8. 《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:一根竹子,原高一丈(1 丈 $ = 10 $ 尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部 3 尺远,问折断处离地面的高度是多少?设折断处离地面的高度为 $ x $ 尺,则可列方程为
$ x ^ { 2 } + 3 ^ { 2 } = ( 10 - x ) ^ { 2 } $
。
答案:
$ x ^ { 2 } + 3 ^ { 2 } = ( 10 - x ) ^ { 2 } $
9. 在 $ \triangle A B C $ 中,$ A B = 15 $,$ A C = 13 $,$ B C $ 边上的高 $ A D = 12 $,则 $ \triangle A B C $ 的周长为
42 或 32
。
答案:
42 或 32
10. 无盖圆柱形杯子的展开图如图所示。将一根长为 $ 20 \mathrm { cm } $ 的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有____
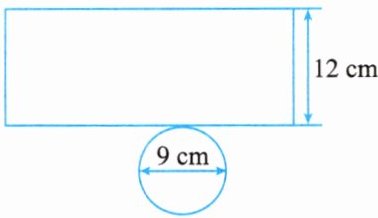
5
$\mathrm { cm } $。
答案:
5
11. 自 2024 年以来,昆明市建起了多个“口袋公园”,它们既美化了城市空间,又拓展了市民的公共活动场所,还体现着城市风貌和文化。如图所示,在某小区旁有一块四边形空地,其中 $ \angle B = 90 ^ { \circ } $,$ A B = 20 \mathrm { m } $,$ B C = 15 \mathrm { m } $,$ A D = 24 \mathrm { m } $,$ C D = 7 \mathrm { m } $。
(1)如图所示,连接 $ A C $,试求 $ A C $ 的长;
(2)昆明市计划将其打造为“口袋公园”,经测算,每平方米的费用为 2 000 元,请你计算将这块地打造成“口袋公园”需要多少钱?
(1)∵在 Rt△ABC中,∠B= 90°,AB=20,BC=15,
∴AC= \sqrt{AB²+BC²}=
答:AC的长为25米
(2) $ \because $ 在 $ \triangle A C D $ 中,$ A D = 24 $,$ C D = 7 $,$ A C = 25 $,
$ \therefore A D ^ { 2 } + C D ^ { 2 } = 24 ^ { 2 } + 7 ^ { 2 } = 625 $.
$ \because A C ^ { 2 } = 25 ^ { 2 } = 625 $,$ \therefore A D ^ { 2 } + C D ^ { 2 } = A C ^ { 2 } $.
$ \therefore \triangle A C D $ 为直角三角形,且 $ \angle D = 90 ^ { \circ } $.
$ \therefore S _ { \text { 四边形 } A B C D } = S _ { \text { Rt } \triangle A B C } + S _ { \text { Rt } \triangle A C D } =
$ \therefore 234 × 2000 =
答:将这块地打造成“口袋公园”需要 468 000 元钱.
(1)如图所示,连接 $ A C $,试求 $ A C $ 的长;
(2)昆明市计划将其打造为“口袋公园”,经测算,每平方米的费用为 2 000 元,请你计算将这块地打造成“口袋公园”需要多少钱?
(1)∵在 Rt△ABC中,∠B= 90°,AB=20,BC=15,
∴AC= \sqrt{AB²+BC²}=
25
(\mathrm {m}).答:AC的长为25米
(2) $ \because $ 在 $ \triangle A C D $ 中,$ A D = 24 $,$ C D = 7 $,$ A C = 25 $,
$ \therefore A D ^ { 2 } + C D ^ { 2 } = 24 ^ { 2 } + 7 ^ { 2 } = 625 $.
$ \because A C ^ { 2 } = 25 ^ { 2 } = 625 $,$ \therefore A D ^ { 2 } + C D ^ { 2 } = A C ^ { 2 } $.
$ \therefore \triangle A C D $ 为直角三角形,且 $ \angle D = 90 ^ { \circ } $.
$ \therefore S _ { \text { 四边形 } A B C D } = S _ { \text { Rt } \triangle A B C } + S _ { \text { Rt } \triangle A C D } =
234
\left( \mathrm { m } ^ { 2 } \right) $.$ \therefore 234 × 2000 =
468000
$ (元).答:将这块地打造成“口袋公园”需要 468 000 元钱.
答案:
$解:(1)∵在 Rt△ABC中,∠B= 90°,AB=20,BC=15,$
(2) $ \because $ 在 $ \triangle A C D $ 中,$ A D = 24 $,$ C D = 7 $,$ A C = 25 $,
$ \therefore A D ^ { 2 } + C D ^ { 2 } = 24 ^ { 2 } + 7 ^ { 2 } = 625 $.
$ \because A C ^ { 2 } = 25 ^ { 2 } = 625 $,$ \therefore A D ^ { 2 } + C D ^ { 2 } = A C ^ { 2 } $.
$ \therefore \triangle A C D $ 为直角三角形,且 $ \angle D = 90 ^ { \circ } $.
$ \therefore S _ { \text { 四边形 } A B C D } = S _ { \text { Rt } \triangle A B C } + S _ { \text { Rt } \triangle A C D } = 234 \left( \mathrm { m } ^ { 2 } \right) $.
$ \therefore 234 \times 2000 = 468000 $ (元).
答:将这块地打造成“口袋公园”需要 468 000 元钱.
$∴AC= \sqrt{AB²+BC²}=25(\mathrm {m}).$
答:AC的长为25米
(2) $ \because $ 在 $ \triangle A C D $ 中,$ A D = 24 $,$ C D = 7 $,$ A C = 25 $,
$ \therefore A D ^ { 2 } + C D ^ { 2 } = 24 ^ { 2 } + 7 ^ { 2 } = 625 $.
$ \because A C ^ { 2 } = 25 ^ { 2 } = 625 $,$ \therefore A D ^ { 2 } + C D ^ { 2 } = A C ^ { 2 } $.
$ \therefore \triangle A C D $ 为直角三角形,且 $ \angle D = 90 ^ { \circ } $.
$ \therefore S _ { \text { 四边形 } A B C D } = S _ { \text { Rt } \triangle A B C } + S _ { \text { Rt } \triangle A C D } = 234 \left( \mathrm { m } ^ { 2 } \right) $.
$ \therefore 234 \times 2000 = 468000 $ (元).
答:将这块地打造成“口袋公园”需要 468 000 元钱.
12. 阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的 2 倍的三角形叫作奇异三角形。
小华:等边三角形一定是奇异三角形!并做了如下证明:
设等边三角形的边长为 $ a $。
$ \because a ^ { 2 } + a ^ { 2 } = 2 a ^ { 2 } $,$ \therefore $ 等边三角形一定是奇异三角形。
小明:那直角三角形中是否存在奇异三角形呢?
(1)在 $ \mathrm { Rt } \triangle A B C $ 中,两边长分别是 $ a = 5 \sqrt { 2 } $,$ c = 10 $,这个三角形是否是奇异三角形?请说明理由;
① 当 c 为斜边时,$ \mathrm { Rt } \triangle A B C $ 不是奇异三角形.理由如下:
当 c 为斜边时,$ b = \sqrt { c ^ { 2 } - a ^ { 2 } } = 5 \sqrt { 2 } $,
$ \therefore a = b $.
$ \therefore a ^ { 2 } + c ^ { 2 } \neq 2 b ^ { 2 } $ (或 $ b ^ { 2 } + c ^ { 2 } \neq 2 a ^ { 2 } $).
$ \therefore \mathrm { Rt } \triangle A B C $ 不是奇异三角形;
② 当 b 为斜边时,$ \mathrm { Rt } \triangle A B C $ 是奇异三角形.理由如下:
当 b 为斜边时,$ b = \sqrt { c ^ { 2 } + a ^ { 2 } } = 5 \sqrt { 6 } $,
$ \because a ^ { 2 } + b ^ { 2 } = 200 $,$ 2 c ^ { 2 } = 200 $,$ \therefore a ^ { 2 } + b ^ { 2 } = 2 c ^ { 2 } $.
$ \therefore \mathrm { Rt } \triangle A B C $ 是奇异三角形
(2)在 $ \mathrm { Rt } \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ A B = c $,$ A C = b $,$ B C = a $,且 $ b > a $。若 $ \mathrm { Rt } \triangle A B C $ 是奇异三角形,求 $ a : b : c $ 的值。
老师:我们新定义一种三角形,两边平方和等于第三边平方的 2 倍的三角形叫作奇异三角形。
小华:等边三角形一定是奇异三角形!并做了如下证明:
设等边三角形的边长为 $ a $。
$ \because a ^ { 2 } + a ^ { 2 } = 2 a ^ { 2 } $,$ \therefore $ 等边三角形一定是奇异三角形。
小明:那直角三角形中是否存在奇异三角形呢?
(1)在 $ \mathrm { Rt } \triangle A B C $ 中,两边长分别是 $ a = 5 \sqrt { 2 } $,$ c = 10 $,这个三角形是否是奇异三角形?请说明理由;
① 当 c 为斜边时,$ \mathrm { Rt } \triangle A B C $ 不是奇异三角形.理由如下:
当 c 为斜边时,$ b = \sqrt { c ^ { 2 } - a ^ { 2 } } = 5 \sqrt { 2 } $,
$ \therefore a = b $.
$ \therefore a ^ { 2 } + c ^ { 2 } \neq 2 b ^ { 2 } $ (或 $ b ^ { 2 } + c ^ { 2 } \neq 2 a ^ { 2 } $).
$ \therefore \mathrm { Rt } \triangle A B C $ 不是奇异三角形;
② 当 b 为斜边时,$ \mathrm { Rt } \triangle A B C $ 是奇异三角形.理由如下:
当 b 为斜边时,$ b = \sqrt { c ^ { 2 } + a ^ { 2 } } = 5 \sqrt { 6 } $,
$ \because a ^ { 2 } + b ^ { 2 } = 200 $,$ 2 c ^ { 2 } = 200 $,$ \therefore a ^ { 2 } + b ^ { 2 } = 2 c ^ { 2 } $.
$ \therefore \mathrm { Rt } \triangle A B C $ 是奇异三角形
(2)在 $ \mathrm { Rt } \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ A B = c $,$ A C = b $,$ B C = a $,且 $ b > a $。若 $ \mathrm { Rt } \triangle A B C $ 是奇异三角形,求 $ a : b : c $ 的值。
$ 1 : \sqrt { 2 } : \sqrt { 3 } $
答案:
解:
(1) ① 当 c 为斜边时,$ \mathrm { Rt } \triangle A B C $ 不是奇异三角形.理由如下:
当 c 为斜边时,$ b = \sqrt { c ^ { 2 } - a ^ { 2 } } = 5 \sqrt { 2 } $,
$ \therefore a = b $.
$ \therefore a ^ { 2 } + c ^ { 2 } \neq 2 b ^ { 2 } $ (或 $ b ^ { 2 } + c ^ { 2 } \neq 2 a ^ { 2 } $).
$ \therefore \mathrm { Rt } \triangle A B C $ 不是奇异三角形;
② 当 b 为斜边时,$ \mathrm { Rt } \triangle A B C $ 是奇异三角形.理由如下:
当 b 为斜边时,$ b = \sqrt { c ^ { 2 } + a ^ { 2 } } = 5 \sqrt { 6 } $,
$ \because a ^ { 2 } + b ^ { 2 } = 200 $,$ 2 c ^ { 2 } = 200 $,$ \therefore a ^ { 2 } + b ^ { 2 } = 2 c ^ { 2 } $.
$ \therefore \mathrm { Rt } \triangle A B C $ 是奇异三角形;
(2) 在 $ \mathrm { Rt } \triangle A B C $ 中,$ a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $,
$ \because c > b > a > 0 $,
$ \therefore 2 c ^ { 2 } > a ^ { 2 } + b ^ { 2 } $,$ 2 a ^ { 2 } < b ^ { 2 } + c ^ { 2 } $.
$ \because \mathrm { Rt } \triangle A B C $ 是奇异三角形,
$ \therefore a ^ { 2 } + c ^ { 2 } = 2 b ^ { 2 } $.$ \therefore 2 b ^ { 2 } = a ^ { 2 } + ( a ^ { 2 } + b ^ { 2 } ) $.
$ \therefore b ^ { 2 } = 2 a ^ { 2 } $.$ \therefore b = \sqrt { 2 } a $.
$ \because c ^ { 2 } = a ^ { 2 } + b ^ { 2 } = 3 a ^ { 2 } $,$ \therefore c = \sqrt { 3 } a $.
$ \therefore a : b : c = 1 : \sqrt { 2 } : \sqrt { 3 } $.
(1) ① 当 c 为斜边时,$ \mathrm { Rt } \triangle A B C $ 不是奇异三角形.理由如下:
当 c 为斜边时,$ b = \sqrt { c ^ { 2 } - a ^ { 2 } } = 5 \sqrt { 2 } $,
$ \therefore a = b $.
$ \therefore a ^ { 2 } + c ^ { 2 } \neq 2 b ^ { 2 } $ (或 $ b ^ { 2 } + c ^ { 2 } \neq 2 a ^ { 2 } $).
$ \therefore \mathrm { Rt } \triangle A B C $ 不是奇异三角形;
② 当 b 为斜边时,$ \mathrm { Rt } \triangle A B C $ 是奇异三角形.理由如下:
当 b 为斜边时,$ b = \sqrt { c ^ { 2 } + a ^ { 2 } } = 5 \sqrt { 6 } $,
$ \because a ^ { 2 } + b ^ { 2 } = 200 $,$ 2 c ^ { 2 } = 200 $,$ \therefore a ^ { 2 } + b ^ { 2 } = 2 c ^ { 2 } $.
$ \therefore \mathrm { Rt } \triangle A B C $ 是奇异三角形;
(2) 在 $ \mathrm { Rt } \triangle A B C $ 中,$ a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $,
$ \because c > b > a > 0 $,
$ \therefore 2 c ^ { 2 } > a ^ { 2 } + b ^ { 2 } $,$ 2 a ^ { 2 } < b ^ { 2 } + c ^ { 2 } $.
$ \because \mathrm { Rt } \triangle A B C $ 是奇异三角形,
$ \therefore a ^ { 2 } + c ^ { 2 } = 2 b ^ { 2 } $.$ \therefore 2 b ^ { 2 } = a ^ { 2 } + ( a ^ { 2 } + b ^ { 2 } ) $.
$ \therefore b ^ { 2 } = 2 a ^ { 2 } $.$ \therefore b = \sqrt { 2 } a $.
$ \because c ^ { 2 } = a ^ { 2 } + b ^ { 2 } = 3 a ^ { 2 } $,$ \therefore c = \sqrt { 3 } a $.
$ \therefore a : b : c = 1 : \sqrt { 2 } : \sqrt { 3 } $.
查看更多完整答案,请扫码查看


