1. 已知小球从点A运动到点B,速度$v(m/s)$是时间$t(s)$的正比例函数,3s时小球的速度是6m/s,那么速度v与时间t之间的关系式是(
A. $v=\frac {t}{3}$
B. $v=\frac {t}{2}$
C. $v=3t$
D. $v=2t$
D
)A. $v=\frac {t}{3}$
B. $v=\frac {t}{2}$
C. $v=3t$
D. $v=2t$
答案:
D
2. 某社区有一块空地需要绿化,一绿化组承担了此项任务,该绿化组工作一段时间后,提高了工作效率。该绿化组完成的绿化面积S(单位:$m^{2}$)与工作时间t(单位:h)之间的函数关系如图所示。该绿化组提高工作效率前每小时完成的绿化面积是(
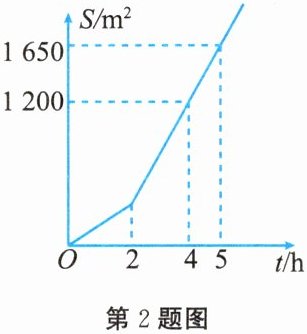
A. $300m^{2}$
B. $150m^{2}$
C. $330m^{2}$
D. $450m^{2}$
B
)
A. $300m^{2}$
B. $150m^{2}$
C. $330m^{2}$
D. $450m^{2}$
答案:
B
3. 8个边长为1的正方形如图所示摆放在平面直角坐标系中,经过原点的一条直线l将这8个正方形分成面积相等的两部分,则该直线l的解析式为(
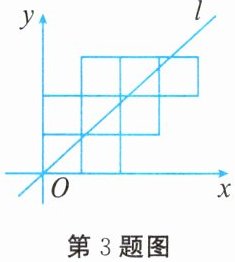
A. $y=\frac {3}{5}x$
B. $y=\frac {3}{4}x$
C. $y=\frac {9}{10}x$
D. $y=x$
C
)
A. $y=\frac {3}{5}x$
B. $y=\frac {3}{4}x$
C. $y=\frac {9}{10}x$
D. $y=x$
答案:
C
4. 龟兔首次赛跑之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场。如图所示的函数图象刻画了龟兔再次赛跑的故事(x表示乌龟从起点出发所行的时间,$y_{1}$表示乌龟所行的路程,$y_{2}$表示兔子所行的路程)。有下列说法:①龟兔再次赛跑的路程为1000m;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10min;④兔子在途中750m处追上乌龟。其中正确的说法有(
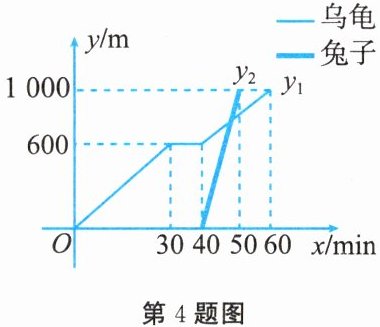
A. ①②③
B. ①②④
C. ①③④
D. ②③④
C
)
A. ①②③
B. ①②④
C. ①③④
D. ②③④
答案:
C
5. 已知一支蜡烛长20cm,每小时燃烧4cm,设剩下的蜡烛的长度为ycm,蜡烛燃烧了xh,则y与x的函数关系式是
$ y = -4x + 20 $
,自变量x的取值范围是$ 0 \leqslant x \leqslant 5 $
。
答案:
$ y = -4x + 20 $ $ 0 \leqslant x \leqslant 5 $
6. 如图所示,已知正比例函数$y_{1}=\frac {1}{2}x$与一次函数$y_{2}=-x+b$的图象交于点P,点P的横坐标为-2,则由图可知方程组$\left\{\begin{array}{l} \frac {1}{2}x-y=0,\\ x+y=b\end{array}\right. $的解为
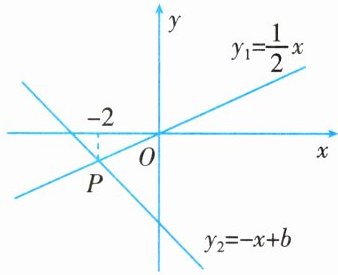
$ \begin{cases} x = -2, \\ y = -1. \end{cases} $
。
答案:
$ \begin{cases} x = -2, \\ y = -1. \end{cases} $
查看更多完整答案,请扫码查看


