1. 函数$y=\frac{\sqrt{x + 1}}{x^{2}-4}$中,自变量$x$的取值范围为(
A. $x\geqslant - 1$
B. $x\geqslant - 1$且$x\neq 2$
C. $x\neq \pm 2$
D. $x>-1$且$x\neq 2$
B
)A. $x\geqslant - 1$
B. $x\geqslant - 1$且$x\neq 2$
C. $x\neq \pm 2$
D. $x>-1$且$x\neq 2$
答案:
1. B
2. 下列各式中,运算正确的是(
A. $\sqrt{8}-\sqrt{2}=\sqrt{6}$
B. $\sqrt{(-2)^{2}}=-2$
C. $\sqrt{\frac{3}{16}}=\frac{\sqrt{3}}{4}$
D. $2\sqrt{3}\times 3\sqrt{3}=6\sqrt{3}$
C
)A. $\sqrt{8}-\sqrt{2}=\sqrt{6}$
B. $\sqrt{(-2)^{2}}=-2$
C. $\sqrt{\frac{3}{16}}=\frac{\sqrt{3}}{4}$
D. $2\sqrt{3}\times 3\sqrt{3}=6\sqrt{3}$
答案:
2. C
3. 如图所示,在$□ ABCD$中,$BF$平分$\angle ABC$,交$AD$于点$F$,$CE$平分$\angle BCD$,交$AD$于点$E$. 若$AB = 6$,$EF = 2$,则$BC$的长为(
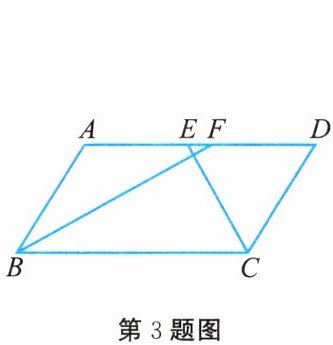
A. 8
B. 10
C. 12
D. 14
B
)
A. 8
B. 10
C. 12
D. 14
答案:
3. B
4. 如图所示,一艘轮船和一艘渔船同时沿各自的航向从港口$O$出发,轮船从港口$O$沿北偏西$20^{\circ}$的方向航行$60$海里到达点$M$处,同一时刻渔船已航行到与港口$O$相距$80$海里的点$N$处. 若$M$,$N$两点相距$100$海里,则$\angle NOF$的度数为(
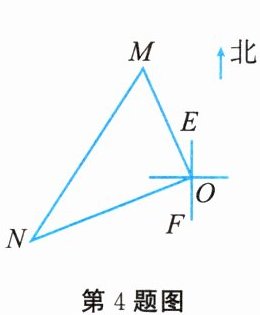
A. $50^{\circ}$
B. $60^{\circ}$
C. $70^{\circ}$
D. $80^{\circ}$
C
)
A. $50^{\circ}$
B. $60^{\circ}$
C. $70^{\circ}$
D. $80^{\circ}$
答案:
4. C
5. 把直线$y = 6x$向上平移后得到直线$AB$. 若直线$AB$经过点$(m,n)$,且$n - 6m = 4$,则直线$AB$的表达式为(
A. $y=-6x + 4$
B. $y=-6x-4$
C. $y = 6x-4$
D. $y = 6x + 4$
D
)A. $y=-6x + 4$
B. $y=-6x-4$
C. $y = 6x-4$
D. $y = 6x + 4$
答案:
5. D
6. 如图所示,四边形$ABCD$的对角线$AC$与$BD$互相垂直. 若$AB = 3$,$BC = 4$,$CD = 5$,则$AD$的长为(
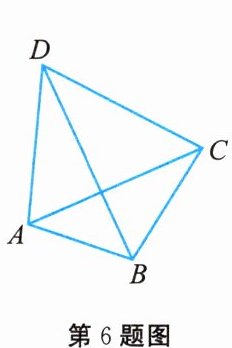
A. $3\sqrt{2}$
B. 4
C. $2\sqrt{3}$
D. $4\sqrt{2}$
A
)
A. $3\sqrt{2}$
B. 4
C. $2\sqrt{3}$
D. $4\sqrt{2}$
答案:
6. A
7. 如图所示,在四边形$ABCD$中,$\angle ABC = 90^{\circ}$,点$E$,$F$分别是$AC$,$AD$的中点,且$BE = EF$. 若$AB = 8$,$BC = 4$,则$CD$的长为(
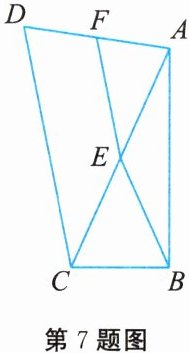
A. $2\sqrt{5}$
B. $4\sqrt{3}$
C. 8
D. $4\sqrt{5}$
D
)
A. $2\sqrt{5}$
B. $4\sqrt{3}$
C. 8
D. $4\sqrt{5}$
答案:
7. D
查看更多完整答案,请扫码查看


