14. “双碳”背景下,新能源汽车在主流的大众消费群体中越来越受欢迎. 在会展中心举行的一场新能源汽车车展活动中,共有三十几种不同品牌的新能源汽车参展,根据不同续航里程将这些车分成六组,统计结果如下:
|分组|A|B|C|D|E|F|
|----|----|----|----|----|----|----|
|续航里程(单位:公里)|$x\leqslant 400$|$400<x\leqslant 500$|$500<x\leqslant 600$|$600<x\leqslant 700$|$700<x\leqslant 800$|$x>800$|
|数量(单位:辆)|40|120|132|95|68|45|
(1)在参展的新能源汽车中,续航里程在
(2)小渡家看中了售价一样的甲、乙两款汽车,根据汽车鉴定机构发布的数据对这两款车的续航里程、百公里加速、智能化水平三项性能进行了打分(百分制),如下表:
| |续航里程(分)|百公里加速(分)|智能化水平(分)|
|----|----|----|----|
|甲车|82|90|100|
|乙车|80|100|90|
小渡将续航里程、百公里加速、智能化水平三项性能的得分按$5:2:3$的比例确定甲、乙两款汽车的最终得分,并以此为依据作出了选择,你知道小渡的选择是什么吗?请写出计算过程进行说明.
|分组|A|B|C|D|E|F|
|----|----|----|----|----|----|----|
|续航里程(单位:公里)|$x\leqslant 400$|$400<x\leqslant 500$|$500<x\leqslant 600$|$600<x\leqslant 700$|$700<x\leqslant 800$|$x>800$|
|数量(单位:辆)|40|120|132|95|68|45|
(1)在参展的新能源汽车中,续航里程在
C
组的车最多;续航里程的中位数落在C
组;(2)小渡家看中了售价一样的甲、乙两款汽车,根据汽车鉴定机构发布的数据对这两款车的续航里程、百公里加速、智能化水平三项性能进行了打分(百分制),如下表:
| |续航里程(分)|百公里加速(分)|智能化水平(分)|
|----|----|----|----|
|甲车|82|90|100|
|乙车|80|100|90|
小渡将续航里程、百公里加速、智能化水平三项性能的得分按$5:2:3$的比例确定甲、乙两款汽车的最终得分,并以此为依据作出了选择,你知道小渡的选择是什么吗?请写出计算过程进行说明.
答案:
14. 解:
(1)C C
(2)小渡选择甲车. 理由如下:
∵89>87,
∴小渡选择甲车.
(1)C C
(2)小渡选择甲车. 理由如下:
甲车综合得分为$82×\frac{5}{5+2+3}+90× \frac{2}{5+2+3}+100×\frac{3}{5+2+3}=89(分),$
乙车综合得分为$80×\frac{5}{5+2+3}+100× \frac{2}{5+2+3}+90×\frac{3}{5+2+3}=87(分),$
∵89>87,
∴小渡选择甲车.
15. 如图所示,矩形$OABC$的顶点$A$,$C$分别在$x$轴,$y$轴的正半轴上,点$B$的坐标为$(15,21)$,一次函数$y = -\frac{3}{5}x + 15$的图象与边$OC$,$AB$分别交于$D$,$E$两点,点$M$是线段$DE$上的一个动点.
(1)求证:$OD = BE$;
(2)连接$OM$,若三角形$ODM$的面积为$\frac{75}{2}$,求点$M$的坐标;
(3)在第(2)问的基础上,设点$P$是$x$轴上一动点,点$Q$是平面内的一点,以$O$,$M$,$P$,$Q$为顶点的四边形是菱形,直接写出点$Q$的坐标.
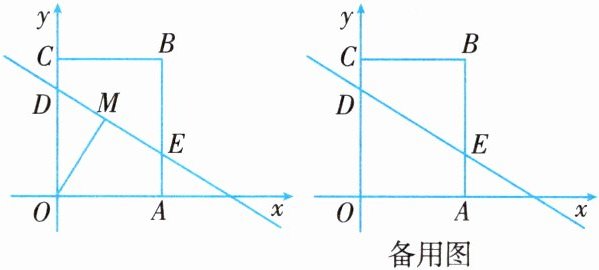
(1)证明:∵点B(15,21),∴C(0,21),A(15,0).设D点坐标为(0,a),E点坐标为(15,b).∴a=-\frac{3}{5}×0+15=15,b=-\frac{3}{5}×15+ 15=6.∴D(0,15),E(15,6).∴OD=15,BE=AB-AE=21-6=15.∴OD=BE.
(2)解:设$M(x, -\frac{3}{5}x + 15)$.
∵$S_{\triangle ODM} = \frac{75}{2}$,$S_{\triangle ODM} = \frac{1}{2}OD·|x_{M}|$,
∴$\frac{1}{2}×15x = \frac{75}{2}$,解得$x = 5$.
∴点$M$的坐标为
(3)点$Q$的坐标为
(1)求证:$OD = BE$;
(2)连接$OM$,若三角形$ODM$的面积为$\frac{75}{2}$,求点$M$的坐标;
(3)在第(2)问的基础上,设点$P$是$x$轴上一动点,点$Q$是平面内的一点,以$O$,$M$,$P$,$Q$为顶点的四边形是菱形,直接写出点$Q$的坐标.

(1)证明:∵点B(15,21),∴C(0,21),A(15,0).设D点坐标为(0,a),E点坐标为(15,b).∴a=-\frac{3}{5}×0+15=15,b=-\frac{3}{5}×15+ 15=6.∴D(0,15),E(15,6).∴OD=15,BE=AB-AE=21-6=15.∴OD=BE.
(2)解:设$M(x, -\frac{3}{5}x + 15)$.
∵$S_{\triangle ODM} = \frac{75}{2}$,$S_{\triangle ODM} = \frac{1}{2}OD·|x_{M}|$,
∴$\frac{1}{2}×15x = \frac{75}{2}$,解得$x = 5$.
∴点$M$的坐标为
(5,12)
;(3)点$Q$的坐标为
(-8,12)或(18,12)或(5, -12)或(-\frac{119}{10},12)
.
答案:
$15. (1)证明:∵点B(15,21),$
(2)解:设$M(x, -\frac{3}{5}x + 15)$.
∵$S_{\triangle ODM} = \frac{75}{2}$,$S_{\triangle ODM} = \frac{1}{2}OD·|x_{M}|$,
∴$\frac{1}{2}×15x = \frac{75}{2}$,解得$x = 5$.
∴点$M$的坐标为$(5,12)$;
(3)点$Q$的坐标为$(-8,12)$或$(18,12)$或$(5, -12)$或$(-\frac{119}{10},12)$. [提示:①当以$OM$为边时;②当以$OM$为对角线时.]
$∴C(0,21),A(15,0).$
$设D点坐标为(0,a),E点坐标为(15,b).$
$∴a=-\frac{3}{5}×0+15=15,b=-\frac{3}{5}×15+ 15=6.$
$∴D(0,15),E(15,6).$
$∴OD=15,BE=AB-AE=21-6=15.$
$∴OD=BE.$
(2)解:设$M(x, -\frac{3}{5}x + 15)$.
∵$S_{\triangle ODM} = \frac{75}{2}$,$S_{\triangle ODM} = \frac{1}{2}OD·|x_{M}|$,
∴$\frac{1}{2}×15x = \frac{75}{2}$,解得$x = 5$.
∴点$M$的坐标为$(5,12)$;
(3)点$Q$的坐标为$(-8,12)$或$(18,12)$或$(5, -12)$或$(-\frac{119}{10},12)$. [提示:①当以$OM$为边时;②当以$OM$为对角线时.]
查看更多完整答案,请扫码查看


