《2025年暑假活动实践与思考八年级理综通用版》

1. 已知函数 $ y = kx(k \neq 0,k $ 为常数)的函数值 $ y $ 随 $ x $ 的增大而减小,那么这个函数的图象可能经过的点是 (C)
A. $ (0.5,1) $
B. $ (2,1) $
C. $ (-2,4) $
D. $ (-2,-2) $

答案： C

2. 若 $ kb \lt 0 $,则函数 $ y = kx + b $ 的图象可能是 (B)

答案： B

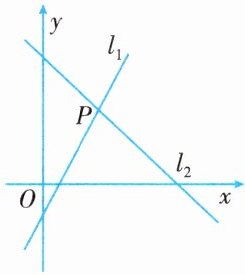
3. 如图所示,直线 $ l_1:y = kx - 1(k \neq 0) $ 与直线 $ l_2:y = -x + 5 $ 相交于点 $ P(2,m) $. 则关于 $ x $ 的不等式 $ kx - 1 \geq -x + 5 $ 的解集为 (C)

A. $ x \gt 2 $
B. $ x \lt 2 $
C. $ x \geq 2 $
D. $ x \leq 2 $

答案： C

4. 星期六早晨,蕊蕊妈妈从家里出发去公园锻炼,她连续、匀速走了 $ 60 $ min 后回家,如图所示的折线段 $ OA - AB - BC $ 是她出发后所在位置离家的距离 $ s(km) $ 与行走时间 $ t(min) $ 之间的函数关系. 下列图形中可以大致描述蕊蕊妈妈行走的路线是 (D)

答案： D

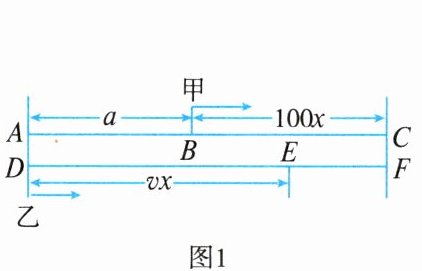
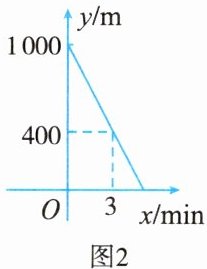
5. 如图 1 所示,甲、乙两人沿江边休闲道同向而行,甲步行的速度为 $ 100 $ m/min,乙骑公共自行车的速度为 $ v $ m/min,起初甲在乙前 $ a $ m 处,两人同时出发,当乙追上甲时,两人停止前行. 设 $ x $ min 后甲、乙两人相距 $ y $ m,$ y $ 与 $ x $ 的函数关系如图 2 所示. 则以下结论: ①图 1 中 $ a $ 表示 $ 1000 $;②图 1 中 $ EF $ 表示 $ 1000 - 200x $;③乙的速度为 $ 200 $ m/min; ④若两人在相距 $ a $ m 处同时相向而行,$ \frac{10}{3} $ min 后相遇. 其中正确的有 (A)


A. ①②
B. ③④
C. ①②③
D. ①③④

答案： A

6. 已知点 $ (-2,y_1),(-1,y_2),(1,y_3) $ 都在直线 $ y = -x + 7 $ 上,则 $ y_1,y_2,y_3 $ 的大小关系是 $ y_{1}＞y_{2}＞y_{3} $.

答案： $ y_{1}＞y_{2}＞y_{3} $