8. 小渡同学匀速地向一个容器内注水,直至注满容器,在注水的过程中,通过观察,小渡画出水面高度 $ h $ 随时间 $ t $ 变化的草图如图所示,则这个容器的形状可能是____

①
(填序号)。
答案:
①
9. 声音在空气中传播的速度 $ y ( \mathrm { m } / \mathrm { s } ) $(简称音速)与气温 $ x ( ^ { \circ } \mathrm { C } ) $ 之间的关系如下表所示,从中可知音速 $ y $ 随温度 $ x $ 的升高而
| 气温 $ x / ^ { \circ } \mathrm { C } $ | 0 | 5 | 10 | 15 | 20 |
| --- | --- | --- | --- | --- | --- |
| 音速 $ y / ( \mathrm { m } / \mathrm { s } ) $ | 331 | 334 | 337 | 340 | 343 |
加快
。在气温为 $ 20 ^ { \circ } \mathrm { C } $ 的一天举办运动会,某人看到发令枪的烟 $ 0.2 \mathrm { s } $ 后,听到了枪声,则由此可知,这个人距发令地点68.6
米。| 气温 $ x / ^ { \circ } \mathrm { C } $ | 0 | 5 | 10 | 15 | 20 |
| --- | --- | --- | --- | --- | --- |
| 音速 $ y / ( \mathrm { m } / \mathrm { s } ) $ | 331 | 334 | 337 | 340 | 343 |
答案:
加快 68.6
10. 如图 1 所示,在平面直角坐标系中,矩形 $ A B C D $ 在第一象限,且 $ A B // y $ 轴。直线 $ m : y = - x $ 沿 $ x $ 轴正方向平移,被矩形 $ A B C D $ 截得的线段 $ E F $ 的长度 $ l $ 与平移的距离 $ a $ 之间的函数图象如图 2 所示,则矩形 $ A B C D $ 的面积是____

15
。
答案:
15
11. 某生物学习小组正在研究同一盆栽内两种植物的共同生长情况,当他们尝试施用某种药物时,发现会对 $ \mathrm { A } $,$ \mathrm { B } $ 两种植物分别产生促进生长和抑制生长的作用,通过实验,$ \mathrm { A } $,$ \mathrm { B } $ 植物的生长高度 $ y _ { \mathrm { A } } ( \mathrm { cm } ) $,$ y _ { \mathrm { B } } ( \mathrm { cm } ) $ 与药物施用量 $ x ( \mathrm { mg } ) $ 的关系数据统计如下表:
| $ x ( \mathrm { mg } ) $ | 0 | 4 | 6 | 8 | 10 | 14 |
| --- | --- | --- | --- | --- | --- | --- |
| $ y _ { \mathrm { A } } ( \mathrm { cm } ) $ | 25 | 21 | 19 | 16 | 15 | 11 |
| $ y _ { \mathrm { B } } ( \mathrm { cm } ) $ | 10 | 18 | 22 | 26 | 31 | 38 |
(1) 根据以上数据,在右边带网格的平面直角坐标系中通过描点,连线,画出 $ \mathrm { A } $,$ \mathrm { B } $ 植物的生长高度 $ y _ { \mathrm { A } } ( \mathrm { cm } ) $,$ y _ { \mathrm { B } } ( \mathrm { cm } ) $ 与药物施用量 $ x ( \mathrm { mg } ) $ 的函数图象;
(2) 猜想 $ \mathrm { A } $,$ \mathrm { B } $ 植物的生长高度 $ y _ { \mathrm { A } } ( \mathrm { cm } ) $,$ y _ { \mathrm { B } } ( \mathrm { cm } ) $ 与药物施用量 $ x ( \mathrm { mg } ) $ 的函数关系,并分别求出函数关系式;
(3) 同学们研究发现,当两种植物高度差距不超过 $ 5 \mathrm { cm } $ 时,两种植物的生长会处于一种良好的平衡状态,求出满足平衡状态时,该药物施用量 $ x ( \mathrm { mg } ) $ 的取值范围。
| $ x ( \mathrm { mg } ) $ | 0 | 4 | 6 | 8 | 10 | 14 |
| --- | --- | --- | --- | --- | --- | --- |
| $ y _ { \mathrm { A } } ( \mathrm { cm } ) $ | 25 | 21 | 19 | 16 | 15 | 11 |
| $ y _ { \mathrm { B } } ( \mathrm { cm } ) $ | 10 | 18 | 22 | 26 | 31 | 38 |
(1) 根据以上数据,在右边带网格的平面直角坐标系中通过描点,连线,画出 $ \mathrm { A } $,$ \mathrm { B } $ 植物的生长高度 $ y _ { \mathrm { A } } ( \mathrm { cm } ) $,$ y _ { \mathrm { B } } ( \mathrm { cm } ) $ 与药物施用量 $ x ( \mathrm { mg } ) $ 的函数图象;
(2) 猜想 $ \mathrm { A } $,$ \mathrm { B } $ 植物的生长高度 $ y _ { \mathrm { A } } ( \mathrm { cm } ) $,$ y _ { \mathrm { B } } ( \mathrm { cm } ) $ 与药物施用量 $ x ( \mathrm { mg } ) $ 的函数关系,并分别求出函数关系式;
(3) 同学们研究发现,当两种植物高度差距不超过 $ 5 \mathrm { cm } $ 时,两种植物的生长会处于一种良好的平衡状态,求出满足平衡状态时,该药物施用量 $ x ( \mathrm { mg } ) $ 的取值范围。

答案:
解:
(1)函数图象如下:
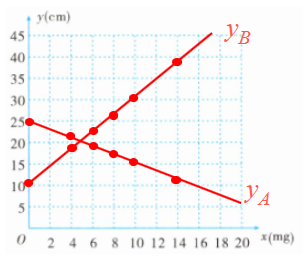
$(2)猜想y_A、y_B与x的函数关系为一次函数,设y_A=k_1x+b_1,y_B=k_2x+b_2,$
$将(0,25)和(14,11)代入y_A=k_1x+b_1,得$
$\begin{cases}{b_1=25}\\{14k_1+b_1=11}\end{cases}$
$解得,\begin{cases}{k_1=-1}\\{b_1=25}\end{cases}$
(3)根据题意,得$ | - x + 25 - (2x + 10) | \leqslant 5 $,解得$ \frac{10}{3} \leqslant x \leqslant \frac{20}{3} $.
∴满足平衡状态时,该药物施用量$ x $(mg)的取值范围为$ \frac{10}{3} \leqslant x \leqslant \frac{20}{3} $.
解:
(1)函数图象如下:

$(2)猜想y_A、y_B与x的函数关系为一次函数,设y_A=k_1x+b_1,y_B=k_2x+b_2,$
$将(0,25)和(14,11)代入y_A=k_1x+b_1,得$
$\begin{cases}{b_1=25}\\{14k_1+b_1=11}\end{cases}$
$解得,\begin{cases}{k_1=-1}\\{b_1=25}\end{cases}$
$将(0,10)和(14,38)代入y_B=k_2x+b_2,得$
$\begin{cases}{b_2=10}\\{14k_2+b_2=38}\end{cases}$
$解得,\begin{cases}{k_2=2}\\{b_2=10}\end{cases}$
$∴y_{A} = -x + 25 $,$ y_{B} = 2x + 10 $;(3)根据题意,得$ | - x + 25 - (2x + 10) | \leqslant 5 $,解得$ \frac{10}{3} \leqslant x \leqslant \frac{20}{3} $.
∴满足平衡状态时,该药物施用量$ x $(mg)的取值范围为$ \frac{10}{3} \leqslant x \leqslant \frac{20}{3} $.
查看更多完整答案,请扫码查看


