7. 已知直线 $ y = kx - 3(k \neq 0) $ 与 $ x $ 轴,$ y $ 轴分别相交于点 $ B $ 和点 $ A $,$ OB = \frac{1}{3}OA $,点 $ C $ 是直线 $ AB $ 上一点且位于第二象限. 当 $ \triangle OBC $ 的面积为 $ 3 $ 时,点 $ C $ 的坐标为 ______
$ (-3,6) $
.
答案:
$ (-3,6) $
8. 如图所示,平面直角坐标系中,点 $ O $ 为坐标原点,点 $ A $ 的坐标为 $ (0,8) $,点 $ B $ 的坐标为 $ (4,0) $,点 $ E $ 是直线 $ y = x + 4 $ 上的一个动点. 若 $ \angle EAB = \angle ABO $,则点 $ E $ 的坐标为
$ (4,8) $或$ (-12,-8) $
.
答案:
$ (4,8) $或$ (-12,-8) $
9. 对于实数 $ a,b $,定义符号 $ \min\{a,b\} $,其意义为: 当 $ a \geq b $ 时,$ \min\{a,b\} = b $;当 $ a \lt b $ 时,$ \min\{a,b\} = a $. 例如:$ \min\{2,-1\} = -1 $,若关于 $ x $ 的函数 $ y = \min\{2x - 1,-x + 3\} $,则该函数的最大值为
$\frac{5}{3}$
.
答案:
$ \frac{5}{3} $
10. 盛夏七月,水果进入丰产季,有甜脆的李子,有可口的荔枝……昆明一水果公司前往水果基地批发水果,设批发李子所需费用 $ y $(单位: 元)与批发数量 $ x $(单位: 千克)的函数关系如图所示;荔枝每千克的价格为 $ 8 $ 元.
(1)求 $ y $ 与 $ x $ 的函数关系式;
(2)该水果店共购买李子和荔枝共 $ 100 $ kg,其中李子数量不少于 $ 70 $ kg,且李子数量不超过荔枝数量的 $ 4 $ 倍,设购买总费用为 $ W $ 元,问:怎样购进这两种水果,才能使总费用最少?
(1)求 $ y $ 与 $ x $ 的函数关系式;
$ y=\left\{\begin{array}{l}6 x, 0 \leqslant x \leqslant 60, \\ 5 x+60, x>60\end{array}\right. $
(2)该水果店共购买李子和荔枝共 $ 100 $ kg,其中李子数量不少于 $ 70 $ kg,且李子数量不超过荔枝数量的 $ 4 $ 倍,设购买总费用为 $ W $ 元,问:怎样购进这两种水果,才能使总费用最少?
购进李子80千克,荔枝20千克,才能使总费用最少.
答案:
$解:(1)当0 \leqslant x \leqslant 60,设y=k_1x,将(60,360)代入,得$
$60k_1=360,解得k_1=6$
$当x>60时,设y=k_2x+b,将(60,360)和(100,560)代入,得$
$\begin{cases}{60k_2+b=360}\\{100k_2+b=560}\end{cases}$
$解得,\begin{cases}{k_2=5}\\{b=60}\end{cases}$
$ y=\left\{\begin{array}{l}6 x, 0 \leqslant x \leqslant 60, \\ 5 x+60, x>60\end{array}\right. $
(2)根据李子批发数量为$ x $千克,可知荔枝批发数量为$ (100-x) $千克.
∵李子数量不少于$ 70 \mathrm{~kg} $,且李子数量不超过荔枝数量的4倍,
$ \therefore\left\{\begin{array}{l}x \geqslant 70, \\ x \leqslant 4(100-x)\end{array}\right. $. 解这个不等式组,得$ 70 \leqslant x \leqslant 80 $.
由题意,得$ W=5 x+60+8(100-x)=-3 x+860 $,
$ \because k=-3<0 $,
$ \therefore W $随$ x $的增大而减小.
$ \therefore $当$ x=80 $时,$ W $最小,且$ W $的最小值为620.
此时,$ 100-x=100-80=20 $(千克).
$ \therefore $购进李子80千克,荔枝20千克,才能使总费用最少.
$60k_1=360,解得k_1=6$
$当x>60时,设y=k_2x+b,将(60,360)和(100,560)代入,得$
$\begin{cases}{60k_2+b=360}\\{100k_2+b=560}\end{cases}$
$解得,\begin{cases}{k_2=5}\\{b=60}\end{cases}$
$ y=\left\{\begin{array}{l}6 x, 0 \leqslant x \leqslant 60, \\ 5 x+60, x>60\end{array}\right. $
(2)根据李子批发数量为$ x $千克,可知荔枝批发数量为$ (100-x) $千克.
∵李子数量不少于$ 70 \mathrm{~kg} $,且李子数量不超过荔枝数量的4倍,
$ \therefore\left\{\begin{array}{l}x \geqslant 70, \\ x \leqslant 4(100-x)\end{array}\right. $. 解这个不等式组,得$ 70 \leqslant x \leqslant 80 $.
由题意,得$ W=5 x+60+8(100-x)=-3 x+860 $,
$ \because k=-3<0 $,
$ \therefore W $随$ x $的增大而减小.
$ \therefore $当$ x=80 $时,$ W $最小,且$ W $的最小值为620.
此时,$ 100-x=100-80=20 $(千克).
$ \therefore $购进李子80千克,荔枝20千克,才能使总费用最少.
11. 如图所示,在平面直角坐标系中,直线 $ y = 2x + 4 $ 与 $ x $ 轴交于点 $ A $,与 $ y $ 轴交于点 $ B $,过点 $ B $ 的直线交 $ x $ 轴正半轴于点 $ C $,且 $ \triangle ABC $ 面积为 $ 10 $.
(1)求点 $ C $ 的坐标及直线 $ BC $ 的解析式;
(2)如图 1 所示,设点 $ F $ 为线段 $ AB $ 的中点,点 $ G $ 为 $ y $ 轴上一动点,连接 $ FG $,以 $ FG $ 为边向 $ FG $ 右侧作正方形 $ FGQP $. 在 $ G $ 点的运动过程中,当顶点 $ Q $ 落在直线 $ BC $ 上时,求点 $ G $ 的坐标.
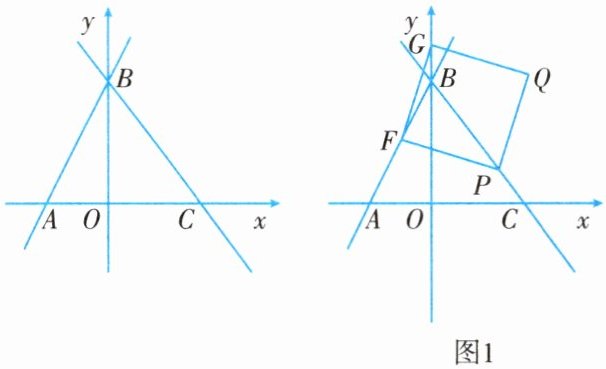
(1)求点 $ C $ 的坐标及直线 $ BC $ 的解析式;
(2)如图 1 所示,设点 $ F $ 为线段 $ AB $ 的中点,点 $ G $ 为 $ y $ 轴上一动点,连接 $ FG $,以 $ FG $ 为边向 $ FG $ 右侧作正方形 $ FGQP $. 在 $ G $ 点的运动过程中,当顶点 $ Q $ 落在直线 $ BC $ 上时,求点 $ G $ 的坐标.

答案:
解:
(1)(过程略)点$ C $的坐标为$ (3,0) $,直线$ BC $的解析式为$ y=-\frac{4}{3} x+4 $;
(2)$ \because $点$ F $为线段$ AB $的中点,$ A(-2,0) $,$ B(0,4) $,$ \therefore F(-1,2) $.
设点$ G $的坐标为$ (0, n) $.
①当$ n>2 $时,如图1所示,若点$ Q $落在$ BC $上时,过$ G $作$ x $轴的平行线,过点$ F $,$ Q $分别作该直线的垂线,垂足分别为$ M $,$ N $.
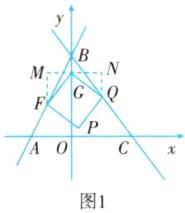
$ \because $四边形$ FGQP $是正方形,一线三垂直,得$ \triangle F M G \cong \triangle G N Q $,
$ \therefore M G=N Q=1 $,$ F M=G N=n-2 $.
$ \therefore Q(n-2, n-1) $.
$ \because Q $点在直线$ y=-\frac{4}{3} x+4 $上,
$ \therefore n-1=-\frac{4}{3}(n-2)+4 $,解得$ n=\frac{23}{7} $.
$ \therefore G\left(0, \frac{23}{7}\right) $;
②当$ n<2 $时,如图2所示,同上,得$ Q(2-n, n+1) $.
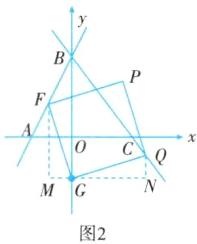
$ \because Q $点在直线$ y=-\frac{4}{3} x+4 $上,
$ \therefore n+1=-\frac{4}{3}(2-n)+4 $,
解得$ n=-1 $. $ \therefore G(0,-1) $.
综上所述,满足条件的点$ G $坐标为$ \left(0, \frac{23}{7}\right) $或$ (0,-1) $.
解:
(1)(过程略)点$ C $的坐标为$ (3,0) $,直线$ BC $的解析式为$ y=-\frac{4}{3} x+4 $;
(2)$ \because $点$ F $为线段$ AB $的中点,$ A(-2,0) $,$ B(0,4) $,$ \therefore F(-1,2) $.
设点$ G $的坐标为$ (0, n) $.
①当$ n>2 $时,如图1所示,若点$ Q $落在$ BC $上时,过$ G $作$ x $轴的平行线,过点$ F $,$ Q $分别作该直线的垂线,垂足分别为$ M $,$ N $.

$ \because $四边形$ FGQP $是正方形,一线三垂直,得$ \triangle F M G \cong \triangle G N Q $,
$ \therefore M G=N Q=1 $,$ F M=G N=n-2 $.
$ \therefore Q(n-2, n-1) $.
$ \because Q $点在直线$ y=-\frac{4}{3} x+4 $上,
$ \therefore n-1=-\frac{4}{3}(n-2)+4 $,解得$ n=\frac{23}{7} $.
$ \therefore G\left(0, \frac{23}{7}\right) $;
②当$ n<2 $时,如图2所示,同上,得$ Q(2-n, n+1) $.

$ \because Q $点在直线$ y=-\frac{4}{3} x+4 $上,
$ \therefore n+1=-\frac{4}{3}(2-n)+4 $,
解得$ n=-1 $. $ \therefore G(0,-1) $.
综上所述,满足条件的点$ G $坐标为$ \left(0, \frac{23}{7}\right) $或$ (0,-1) $.
查看更多完整答案,请扫码查看


