《2025年暑假活动实践与思考八年级理综通用版》

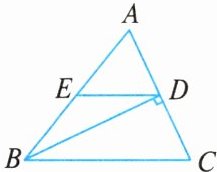
7. 如图所示，在$\triangle ABC$中，$D$是$AC$的中点，且$BD\perp AC$，$ED// BC$，$ED$交$AB$于点$E$，$BC = 7\mathrm{c}\mathrm{m}$，$AC = 6\mathrm{c}\mathrm{m}$，则$\triangle AED$的周长为10$\mathrm{c}\mathrm{m}$.

答案： 10

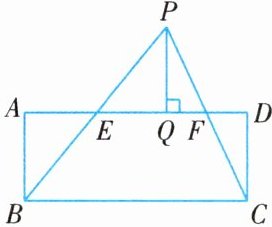
8. 如图所示，在$\triangle PBC$中，分别取$PB$，$PC$的中点$E$，$F$，连接$EF$，过点$P$作$PQ\perp EF$，垂足为$Q$，将$\triangle PBC$分割后拼接成矩形$ABCD$. 若$EF = 4$，$PQ = 3$，则矩形$ABCD$的面积是______24.

答案： 24

9. 若正方形$ABCD$的边长为$4$，$E$是$BC$边上的一点，$BE = 3$，$M$为线段$AE$上的一点，射线$BM$交正方形的一边于点$F$，且$BF = AE$，则$BM =$2.5 或 2.4.

答案： 2.5 或 2.4

10. 已知$\triangle ABC$的三个顶点都是同一个正方形的顶点，$\angle ABC$的平分线与线段$AC$交于点$D$. 若$\triangle ABC$的一条边长为$6$，则点$D$到直线$AB$的距离为3 或 $\frac{3\sqrt{2}}{2}$ 或 $6\sqrt{2}-6$ 或 $6-3\sqrt{2}$.

答案： 3 或 $\frac{3\sqrt{2}}{2}$ 或 $6\sqrt{2}-6$ 或 $6-3\sqrt{2}$

11. 如图所示，在四边形$ABCD$中，$AB = BC$，对角线$BD$平分$\angle ABC$，$P$是$BD$上一点，过点$P$作$PM\perp AD$，$PN\perp CD$，垂足分别为$M$，$N$.
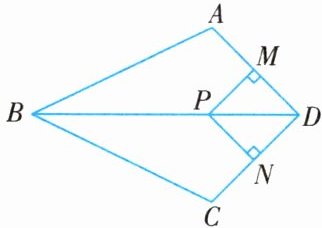
(1) 求证：$\angle ADB = \angle CDB$；
(2) 若$\angle ADC =$______90$^{\circ}$时，四边形$MPND$是正方形，并说明理由.

答案：
(1) 证明: 
∵对角线BD平分∠ABC，
∴∠ABD=∠CBD.

在△ABD和△CBD中，

$\begin{cases}{\ AB=CB，}\\{∠ABD=∠CBD,\ }\\{BD=BD,\ }\end{cases}$

∴△ABD≌△CBD(SAS).

∴∠ADB=∠CDB.

(2) 解: 90. 理由如下:
∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
∵∠ADC=90°,
∴四边形MPND是矩形.
∵∠ADB=∠CDB,
∴∠ADB=45°.
∵∠PMD=90°,
∴∠MPD=∠PDM=45°.
∴PM=MD.
∴矩形MPND是正方形.

12. 在菱形$ABCD$中，$\angle ABC = 60^{\circ}$，点$P$是射线$BD$上一动点，以$AP$为边向右侧作等边$\triangle APE$.
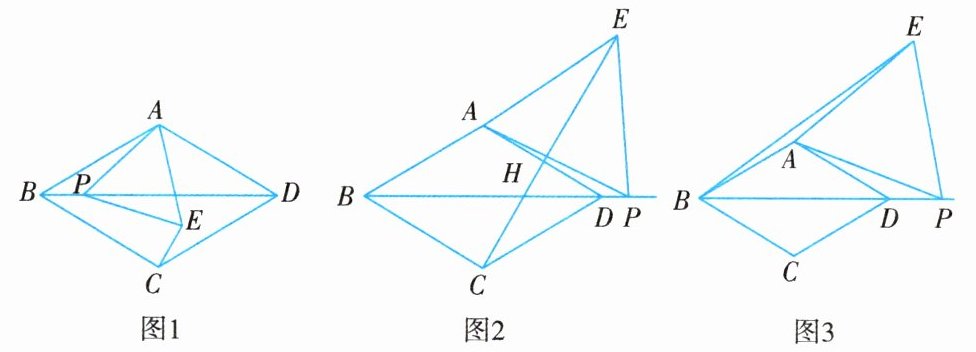
(1) 如图 1 所示，当点$E$在菱形$ABCD$内部或边上时，连接$CE$，则$BP$与$CE$的数量关系是______；$CE$与$AD$的位置关系是______；
(2) 如图 2 所示，当点$E$在菱形$ABCD$外部时，连接$CE$，那么(1)中的结论是否仍成立？若成立，请予以证明；若不成立，请说明理由；
(3) 如图 3 所示，当点$P$在线段$BD$的延长线上时，连接$BE$，若$AB = 4\sqrt{3}$，$BE = 4\sqrt{19}$，请直接写出四边形$ADPE$的面积.

答案：
解:
(1) BP=CE　CE⊥AD
(2) 当点E在菱形ABCD外部时，
(1)中的结论仍成立.证明如下:

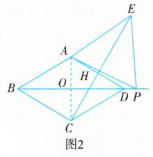
如图2所示，连接AC交BD于点O,设CE 交AD于点H.
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,
∠ABD=∠CBD=30°.
∴AB=AC,∠BAC=60°.
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°.
∴∠BAP=∠CAE.
在△BAP和△CAE中,
∵ $\left\{\begin{array}{l} AB=AC,\\ \angle BAP=\angle CAE,\\ AP=AE,\end{array}\right.$
∴△BAP≌△CAE(SAS).
∴BP=CE,∠ABP=∠ACE=30°.
∵∠CAH=60°,
∴∠CAH+∠ACH=90°.
∴∠AHC=90°.
∴CE⊥AD;
(3) 四边形ADPE的面积为32$\sqrt{3}$.(提示:连接AC交BD于点O,连接CE，过点E作EH⊥AP于点H.)