【活动任务】
我们知道,对于任意一个四边形,连接它的四边的中点所构成的四边形是一个平行四边形.由此,我们自然想到:在什么条件下,连接四边形各边中点所构成的四边形是矩形、菱形或正方形呢?
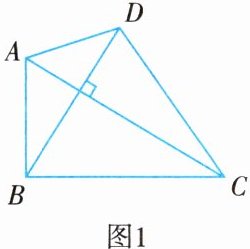
1. 任意画两条互相垂直且相交的线段 $ AC $, $ BD $,并顺次连接四个端点得到四边形 $ ABCD $,如图 1 所示.连接四边形 $ ABCD $ 的各边中点得到四边形 $ EFGH $,如图 2 所示.观察四边形 $ EFGH $,我们能发现它是一个矩形.
2. 任意画两条相等且相交的线段 $ AC $, $ BD $,并顺次连接四个端点得到四边形 $ ABCD $,如图 3 所示.连接四边形 $ ABCD $ 的各边中点得到四边形 $ EFGH $,如图 4 所示,观察四边形 $ EFGH $,我们能发现它是一个菱形.
任务 1:根据以上经验,猜想在一个什么样的四边形中,顺次连接其各边的中点,可以得到一个正方形,请你在下面画出示意图;
任务 2:顺次连接矩形、菱形和正方形各边中点所得到的四边形分别是什么四边形? 提出猜想,并说明你的猜想是否正确.
我们知道,对于任意一个四边形,连接它的四边的中点所构成的四边形是一个平行四边形.由此,我们自然想到:在什么条件下,连接四边形各边中点所构成的四边形是矩形、菱形或正方形呢?
1. 任意画两条互相垂直且相交的线段 $ AC $, $ BD $,并顺次连接四个端点得到四边形 $ ABCD $,如图 1 所示.连接四边形 $ ABCD $ 的各边中点得到四边形 $ EFGH $,如图 2 所示.观察四边形 $ EFGH $,我们能发现它是一个矩形.
2. 任意画两条相等且相交的线段 $ AC $, $ BD $,并顺次连接四个端点得到四边形 $ ABCD $,如图 3 所示.连接四边形 $ ABCD $ 的各边中点得到四边形 $ EFGH $,如图 4 所示,观察四边形 $ EFGH $,我们能发现它是一个菱形.

任务 1:根据以上经验,猜想在一个什么样的四边形中,顺次连接其各边的中点,可以得到一个正方形,请你在下面画出示意图;
任务 2:顺次连接矩形、菱形和正方形各边中点所得到的四边形分别是什么四边形? 提出猜想,并说明你的猜想是否正确.
答案:
任务1:当四边形的对角线相等且互相垂直时,顺次连接其各边的中点,可以得到一个正方形。示意图如下:
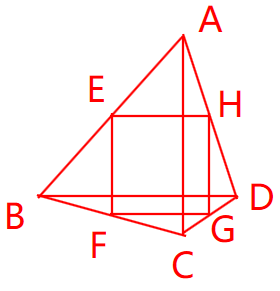
任务2:①顺次连接矩形各边中点所得到的四边形是菱形
设矩形$ABCD$,$E$、$F$、$G$、$H$分别是$AB$、$BC$、$CD$、$DA$的中点,连接$AC$、$BD$。根据三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。在$\triangle ABD$中,因为$E$是$AB$的中点,$H$是$AD$的中点,所以$EH// BD$,$EH = \frac{1}{2}BD$。在$\triangle BCD$中,因为$F$是$BC$的中点,$G$是$CD$的中点,所以$FG// BD$,$FG=\frac{1}{2}BD$。则$EH// FG$,$EH = FG$,所以四边形$EFGH$是平行四边形。又因为矩形的对角线相等,即$AC = BD$,同理可得$EF=\frac{1}{2}AC$,$HG=\frac{1}{2}AC$,所以$EF = EH$。有一组邻边相等的平行四边形是菱形,所以顺次连接矩形各边中点所得到的四边形是菱形。
②顺次连接菱形各边中点所得到的四边形是矩形
设菱形$ABCD$,$E$、$F$、$G$、$H$分别是$AB$、$BC$、$CD$、$DA$的中点,连接$AC$、$BD$。同样根据三角形中位线定理,在$\triangle ABD$中,$EH// BD$,$EH=\frac{1}{2}BD$;在$\triangle BCD$中,$FG// BD$,$FG = \frac{1}{2}BD$,所以$EH// FG$,$EH = FG$,四边形$EFGH$是平行四边形。因为菱形的对角线互相垂直,即$AC\perp BD$,又因为$EF// AC$,$EH// BD$,所以$EF\perp EH$。有一个角是直角的平行四边形是矩形,所以顺次连接菱形各边中点所得到的四边形是矩形。
③顺次连接正方形各边中点所得到的四边形是正方形
设正方形$ABCD$,$E$、$F$、$G$、$H$分别是$AB$、$BC$、$CD$、$DA$的中点,连接$AC$、$BD$。由三角形中位线定理可得,$EH// BD$,$EH=\frac{1}{2}BD$,$FG// BD$,$FG=\frac{1}{2}BD$,$EF// AC$,$EF=\frac{1}{2}AC$,$HG// AC$,$HG=\frac{1}{2}AC$,所以$EH// FG$,$EH = FG$,$EF// HG$,$EF = HG$,四边形$EFGH$是平行四边形。因为正方形的对角线相等且互相垂直,即$AC = BD$,$AC\perp BD$,所以$EF = EH$且$EF\perp EH$。有一组邻边相等且有一个角是直角的平行四边形是正方形,所以顺次连接正方形各边中点所得到的四边形是正方形。
【答案】:顺次连接矩形各边中点所得到的四边形是菱形;顺次连接菱形各边中点所得到的四边形是矩形;顺次连接正方形各边中点所得到的四边形是正方形,猜想正确。
任务1:当四边形的对角线相等且互相垂直时,顺次连接其各边的中点,可以得到一个正方形。示意图如下:

任务2:①顺次连接矩形各边中点所得到的四边形是菱形
设矩形$ABCD$,$E$、$F$、$G$、$H$分别是$AB$、$BC$、$CD$、$DA$的中点,连接$AC$、$BD$。根据三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。在$\triangle ABD$中,因为$E$是$AB$的中点,$H$是$AD$的中点,所以$EH// BD$,$EH = \frac{1}{2}BD$。在$\triangle BCD$中,因为$F$是$BC$的中点,$G$是$CD$的中点,所以$FG// BD$,$FG=\frac{1}{2}BD$。则$EH// FG$,$EH = FG$,所以四边形$EFGH$是平行四边形。又因为矩形的对角线相等,即$AC = BD$,同理可得$EF=\frac{1}{2}AC$,$HG=\frac{1}{2}AC$,所以$EF = EH$。有一组邻边相等的平行四边形是菱形,所以顺次连接矩形各边中点所得到的四边形是菱形。
②顺次连接菱形各边中点所得到的四边形是矩形
设菱形$ABCD$,$E$、$F$、$G$、$H$分别是$AB$、$BC$、$CD$、$DA$的中点,连接$AC$、$BD$。同样根据三角形中位线定理,在$\triangle ABD$中,$EH// BD$,$EH=\frac{1}{2}BD$;在$\triangle BCD$中,$FG// BD$,$FG = \frac{1}{2}BD$,所以$EH// FG$,$EH = FG$,四边形$EFGH$是平行四边形。因为菱形的对角线互相垂直,即$AC\perp BD$,又因为$EF// AC$,$EH// BD$,所以$EF\perp EH$。有一个角是直角的平行四边形是矩形,所以顺次连接菱形各边中点所得到的四边形是矩形。
③顺次连接正方形各边中点所得到的四边形是正方形
设正方形$ABCD$,$E$、$F$、$G$、$H$分别是$AB$、$BC$、$CD$、$DA$的中点,连接$AC$、$BD$。由三角形中位线定理可得,$EH// BD$,$EH=\frac{1}{2}BD$,$FG// BD$,$FG=\frac{1}{2}BD$,$EF// AC$,$EF=\frac{1}{2}AC$,$HG// AC$,$HG=\frac{1}{2}AC$,所以$EH// FG$,$EH = FG$,$EF// HG$,$EF = HG$,四边形$EFGH$是平行四边形。因为正方形的对角线相等且互相垂直,即$AC = BD$,$AC\perp BD$,所以$EF = EH$且$EF\perp EH$。有一组邻边相等且有一个角是直角的平行四边形是正方形,所以顺次连接正方形各边中点所得到的四边形是正方形。
【答案】:顺次连接矩形各边中点所得到的四边形是菱形;顺次连接菱形各边中点所得到的四边形是矩形;顺次连接正方形各边中点所得到的四边形是正方形,猜想正确。
查看更多完整答案,请扫码查看


