《2025年暑假活动实践与思考八年级理综通用版》

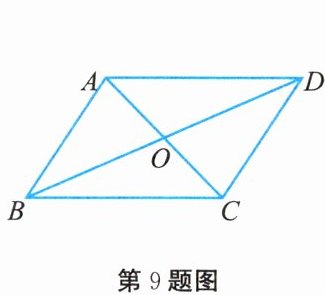
9. 如图所示，要使平行四边形 ABCD 为矩形，则可添加的条件是∠BAD = 90°(或AC = BD等,答案不唯一).

答案： ∠BAD = 90°(或AC = BD等,答案不唯一)

10. 矩形的一条边长为 3 cm，面积为 $12 cm^{2}$，则该矩形的一条对角线长为5cm.

答案： 5

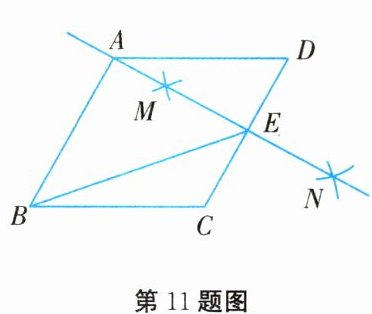
11. 如图所示，在菱形 ABCD 中，$AB = 4$，按以下步骤作图：①分别以点 C 和点 D 为圆心，大于$\frac{1}{2}CD$的长为半径画弧，两弧交于点 M，N；②作直线 MN，且 MN 恰好经过点 A，与 CD 交于点 E，连接 BE，则 BE 的长为2$\sqrt{7}$.

答案： 2$\sqrt{7}$

12. 如图所示，四边形 ABCD 是正方形，点 E 在 BC 边上，点 F 在 CD 的延长线上，满足$BE = DF$，连接 EF 与对角线 BD 交于点 G，连接 AF，AG. 若$AF=\sqrt{10}$，则 AG 的长为________.

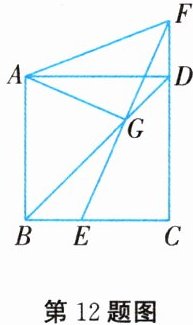
$\sqrt{5}$

答案： $\sqrt{5}$

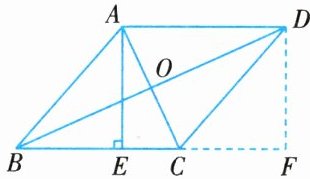
13. 如图所示，在菱形 ABCD 中，对角线 AC，BD 交于点 O，过点 A 作 BC 的垂线，垂足为点 E，延长 BC 到点 F，使$CF = BE$，连接 DF.
（1）求证：四边形 AEFD 是矩形；
（2）若$AB = 13$，$AC = 10$，求 AE 的长.

（1）证明：∵四边形ABCD是菱形，
∴AD//BC且AD=BC.
∵BE=CF，
∴BE+EC=CF+EC，即BC=EF.
∴AD=EF.
∵AD//EF，
∴四边形AEFD是平行四边形.
∵AE⊥BC，
∴∠AEF=90°.
∴四边形AEFD是矩形.
（2）∵四边形ABCD是菱形，
∴AC⊥BD,AO=CO,BO=DO,BC= AB=13,AC=10.
∴AO=CO=5.
在Rt△ABO中，由勾股定理，得
BO=√(AB²-AO²)=√(13²-5²)=12.
∵S△ABC=(1/2)BC·AE=(1/2)AC·BO,
∴(1/2)×13AE=(1/2)×10×12.
∴AE=120/13.
答:AE的长为120/13.

答案：

$证明:(1)∵四边形ABCD是菱形，$

$ ∴AD//BC且AD=BC.$

$∵BE=CF，$

$∴BE+EC=CF+EC，即BC=EF.$

$∴AD=EF.$

$∵AD//EF，$

$∴四边形AEFD是平行四边形.$

$∵AE⊥BC，$

$∴∠AEF=90°.$

$∴四边形AEFD是矩形.$

$(2)∵四边形ABCD是菱形，$

$∴AC⊥BD,AO=CO,BO=DO,BC= AB=13,AC=10.$

$∴AO=CO=\frac{1}{2}AC=5.$

$在Rt△ABO中，由勾股定理，得$

$BO=\sqrt{AB^2-AO^2}= \sqrt{13²-5²}=12.$

$∵S_{△ABC}=\frac{1}{2}BC·AE=\frac{1}{2}AC·BO,$

$∴\frac{1}{2}×13AE=\frac{1}{2}×10×12.$

$∴AE=\frac{120}{13}.$

$答:AE的长为\frac{120}{13}.$

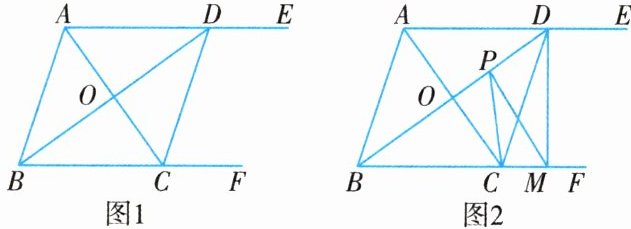
14. 如图 1 所示，$AE// BF$，$AB// DC$，BD 平分$∠ABC$.
（1）求证：四边形 ABCD 是菱形；
（2）如图 2 所示，$CD = 5$，$AC = 6$，$DM⊥BF$于点 M，已知点 P 是 BD 上一动点，连接 PC，PM. 求$△PCM$周长的最小值.

答案：

(1)证明:略;
(2)解:如图2所示，连接PA,AM.
由
(1)知，四边形ABCD是菱形.
∵AC = 6,
∴OC = 3,AC⊥BD.
∵CD = 5,
∴OD = $\sqrt{CD^{2} - OC^{2}}$ = 4.
∴BD = 8.
∵DM⊥BF,
∴S菱形ABCD = BC·DM = $\frac{1}{2}$BD·AC.
∴DM = $\frac{BD·AC}{2BC}$ = $\frac{8×6}{2×5}$ = $\frac{24}{5}$.
∴CM = $\sqrt{CD^{2} - DM^{2}}$ = $\frac{7}{5}$.
∵菱形ABCD关于对角线BD所在直线对称，
∴PA = PC.
∴C△PCM = PC + PM + CM = PA + PM + $\frac{7}{5}$ ≥ AM + $\frac{7}{5}$.
∴△PCM周长的最小值为AM + $\frac{7}{5}$.
在Rt△ADM中,AM = $\sqrt{AD^{2} + DM^{2}}$ = $\sqrt{5^{2} + (\frac{24}{5})^{2}}$ = $\frac{\sqrt{1201}}{5}$,
∴△PCM周长的最小值为$\frac{7 + \sqrt{1201}}{5}$.