9. 如图所示,在 $ □ ABCD $ 中,$ \angle ADC = 119^{\circ} $,$ BE \perp DC $ 于点 $ E $,$ DF \perp BC $ 于点 $ F $,$ BE $ 与 $ DF $ 交于点 $ H $,则 $ \angle BHF = $
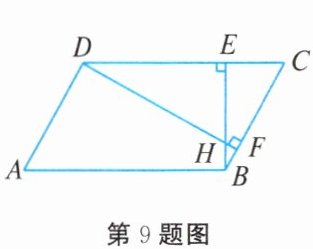
61°
。
答案:
61°
10. 如图所示,在 $ □ ABCD $ 中,$ \angle ABC = 60^{\circ} $,$ E $,$ F $ 分别在 $ CD $ 和 $ BC $ 的延长线上,$ AE // BD $,$ EF \perp BC $,$ EF = 3 $,则 $ AB $ 的长是______
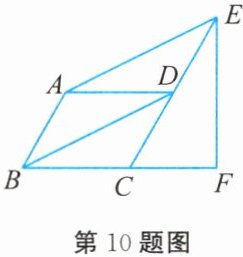
$\sqrt{3}$
。
答案:
$\sqrt{3}$
11. 如图所示,$ □ ABCD $ 的对角线相交于点 $ O $,且 $ AB \neq AD $,过点 $ O $ 作 $ OE \perp BD $ 交 $ BC $ 于点 $ E $。若 $ \triangle CDE $ 的周长为 10,则平行四边形 $ ABCD $ 的周长为
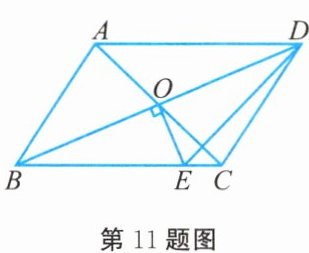
20
。
答案:
20
12. 如图所示,在 $ □ ABCD $ 中,$ \angle C = 60^{\circ} $,点 $ M $,$ N $ 分别是 $ AD $,$ BC $ 的中点,$ BC = 2CD $。
求证:(1) 四边形 $ MNCD $ 是平行四边形;
(2) $ BD = \sqrt{3}MN $。
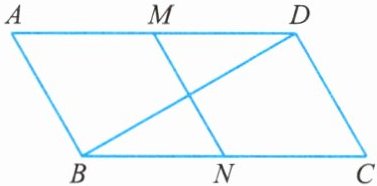
求证:(1) 四边形 $ MNCD $ 是平行四边形;
(2) $ BD = \sqrt{3}MN $。

答案:
证明:
(1)略;
(2)如图所示,连接DN.
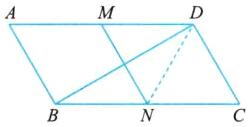
∵点N是BC的中点,$BC = 2CD$,
∴$CD = NC$.
∵$\angle C = 60^{\circ}$,
∴$\triangle DCN$是等边三角形.
∴$\angle DNC = \angle NDC = 60^{\circ}$,$ND = NB = CN$,$\angle DNB = 120^{\circ}$.
∴$\angle DBC = \angle BDN = 30^{\circ}$.
∴$\angle BDC = \angle BDN + \angle NDC = 90^{\circ}$.
∴$BD = \sqrt{BC^{2}-CD^{2}} = \sqrt{(2CD)^{2}-CD^{2}} = \sqrt{3}CD$.
∵四边形MNCD是平行四边形,
∴$MN = CD$.
∴$BD = \sqrt{3}MN$.
证明:
(1)略;
(2)如图所示,连接DN.

∵点N是BC的中点,$BC = 2CD$,
∴$CD = NC$.
∵$\angle C = 60^{\circ}$,
∴$\triangle DCN$是等边三角形.
∴$\angle DNC = \angle NDC = 60^{\circ}$,$ND = NB = CN$,$\angle DNB = 120^{\circ}$.
∴$\angle DBC = \angle BDN = 30^{\circ}$.
∴$\angle BDC = \angle BDN + \angle NDC = 90^{\circ}$.
∴$BD = \sqrt{BC^{2}-CD^{2}} = \sqrt{(2CD)^{2}-CD^{2}} = \sqrt{3}CD$.
∵四边形MNCD是平行四边形,
∴$MN = CD$.
∴$BD = \sqrt{3}MN$.
13. 如图所示,在四边形 $ ABCD $ 中,$ AB // DC $,$ \angle ABC = 90^{\circ} $,$ AD = CD = 13 \mathrm{~cm} $,$ BC = 12 \mathrm{~cm} $。$ M $,$ N $ 是线段 $ AB $,$ CD $ 上两动点,$ M $ 点从点 $ A $ 出发,以每秒 $ 2 \mathrm{~cm} $ 的速度沿 $ AB $ 方向运动,$ N $ 点从点 $ D $ 出发,以每秒 $ 1 \mathrm{~cm} $ 的速度沿 $ DC $ 方向运动,$ M $,$ N $ 同时出发,同时停止。当 $ M $ 运动到点 $ B $ 时,$ M $,$ N $ 同时停止运动,设运动时间为 $ t $ 秒。
(1) 求 $ AB $ 的长;
(2) 当 $ t $ 为何值时,四边形 $ AMCN $ 为平行四边形?
(3) 在 $ M $,$ N $ 运动的过程中,是否存在四边形 $ MBCN $ 是矩形?若存在,请求出 $ t $ 的值;若不存在,请说明理由。
(1) 求 $ AB $ 的长;
(2) 当 $ t $ 为何值时,四边形 $ AMCN $ 为平行四边形?
(3) 在 $ M $,$ N $ 运动的过程中,是否存在四边形 $ MBCN $ 是矩形?若存在,请求出 $ t $ 的值;若不存在,请说明理由。

答案:
解:
(1)(过程略,提示:过点D作DE $ \perp AB$于点E.)AB的长为18cm;
(2)当四边形AMCN为平行四边形时,点M在AB上,点N在DC上,如图2所示,连接AN,CM.
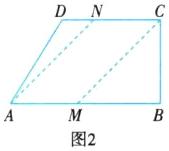
∴$AM = CN$.
由题意,得 $AM = 2t$,$DN = t$,
∴$BM = 18 - 2t$,$CN = 13 - t$.
∴$2t = 13 - t$,解得 $t = \frac{13}{3}$.
∴当 $t = \frac{13}{3}$ 时,四边形AMCN为平行四边形;
(3)在M,N运动的过程中,存在四边形MBCN是矩形. 如图3所示,连接MN.
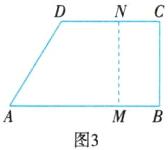
∵$AB // CD$,$\angle ABC = 90^{\circ}$,
∴当 $CN = BM$ 时,四边形MBCN是矩形.
∴$13 - t = 18 - 2t$,解得 $t = 5$.
∴当 $t = 5$ 时,四边形MBCN是矩形.
解:
(1)(过程略,提示:过点D作DE $ \perp AB$于点E.)AB的长为18cm;
(2)当四边形AMCN为平行四边形时,点M在AB上,点N在DC上,如图2所示,连接AN,CM.

∴$AM = CN$.
由题意,得 $AM = 2t$,$DN = t$,
∴$BM = 18 - 2t$,$CN = 13 - t$.
∴$2t = 13 - t$,解得 $t = \frac{13}{3}$.
∴当 $t = \frac{13}{3}$ 时,四边形AMCN为平行四边形;
(3)在M,N运动的过程中,存在四边形MBCN是矩形. 如图3所示,连接MN.

∵$AB // CD$,$\angle ABC = 90^{\circ}$,
∴当 $CN = BM$ 时,四边形MBCN是矩形.
∴$13 - t = 18 - 2t$,解得 $t = 5$.
∴当 $t = 5$ 时,四边形MBCN是矩形.
查看更多完整答案,请扫码查看


