《2025年暑假活动实践与思考八年级理综通用版》

13. 计算:
(1) $ \sqrt { 80 } - \sqrt { 8 } + \sqrt { 45 } + \sqrt { 32 } $; (2) $ \sqrt { 75 } \div \sqrt { 3 } - \sqrt { \frac { 1 } { 2 } } \times \sqrt { 12 } + \sqrt { 54 } $;
(3) $ \left( 2 \sqrt { 108 } - 6 \sqrt { \frac { 1 } { 27 } } \right) \div \sqrt { 3 } $; (4) $ ( 7 - 4 \sqrt { 3 } ) ( 4 \sqrt { 3 } + 7 ) - ( 2 \sqrt { 5 } - 1 ) ^ { 2 } $.

答案： 解：
(1) 原式 $ = 7\sqrt{5} + 2\sqrt{2} $；
(2) 原式 $ = 5 + 2\sqrt{6} $；
(3) 原式 $ = \frac{34}{3} $；
(4) 原式 $ = -20 + 4\sqrt{5} $。

14. 高空抛物现象曾被称为“悬挂城市上空的痛”, 严重威胁着人们的“头顶安全”, 即便是常见小物件, 一旦高空落下, 也威力惊人, 而且用时很短, 常常来不及避让. 据研究, 高空抛物下落的时间 $ t $ (秒) 和高度 $ h $ (米) 近似满足公式 $ t = \sqrt { \frac { 2 h } { g } } $ (其中 $ g \approx 9.8 $ 米/秒 $ ^ { 2 } $ ).
(1) 当 $ h = 98 $ 米时, 求下落的时间 $ t $; (结果精确到 0.01 秒, 参考数据: $ \sqrt { 2 } \approx 1.414, \sqrt { 3 } \approx 1.732, \sqrt { 5 } \approx 2.236 $ )
下落的时间 $ t $ 约等于 4.47秒；
(2) 高空抛物伤害无防护人体只需要 65 焦的动能, 高空抛物动能(焦) $ = 10 × $ 物体质量 (千克) $ × $ 高度(米). 某质量为 0.1 千克的玩具在高空被抛出, 经过 4 秒后落在地上, 这个玩具产生的动能会伤害到楼下的行人吗? 请说明理由.
这个玩具产生的动能会伤害到楼下的行人. 理由如下：
当 $ t = 4 $ 秒时，$ 4 = \sqrt{\frac{2h}{9.8}} $，解得 $ h = 78.4 $。
$ \because 10 × 0.1 × 78.4 = 78.4 $ (焦)，
$ \therefore 78.4 ＞ 65 $。
$ \therefore $ 这个玩具产生的动能会伤害到楼下的行人。

答案： 解：
(1)将$h=98$代入$t=\sqrt {\frac{2h}{g}}$，得
$t=\sqrt {\frac{2×98}{9.8}}≈4.47$
∴下落的时间 $ t $ 约等于 4.47 秒；
(2) 这个玩具产生的动能会伤害到楼下的行人. 理由如下：
当 $ t = 4 $ 秒时，$ 4 = \sqrt{\frac{2h}{9.8}} $，解得 $ h = 78.4 $。
$ \because 10 \times 0.1 \times 78.4 = 78.4 $ (焦)，
$ \therefore 78.4 ＞ 65 $。
$ \therefore $ 这个玩具产生的动能会伤害到楼下的行人。

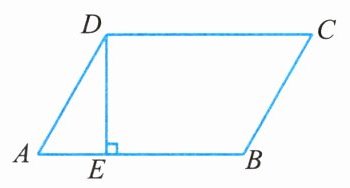
15. 如图所示, 在 $ □ A B C D $ 中, $ D E \perp A B $ 于点 $ E, \angle A = 60 ^ { \circ }, B E = 2 A E = \sqrt { 72 } $ cm. 求 $ □ A B C D $ 的周长和面积.

$ □ A B C D $ 的周长为$30\sqrt{2}$cm，面积为$54\sqrt{3}$cm².

答案：

$解:在Rt△ADE中，由∠A=60°， 得∠ADE=30°，$

$∴AD=2AE= \sqrt{72}=6 \sqrt{2}(\ \mathrm {cm}).$

$根据勾股定理,DE= \sqrt{AD²-AE²}= 3 \sqrt{6}(\ \mathrm {cm}).$

$又∵AB=AE+EB=\frac{\sqrt{72}}{2}+\sqrt{72}= 3 \sqrt{2}+6 \sqrt{2}=9 \sqrt{2}(\ \mathrm {cm})，$

$∴▱ABCD的周长为2(AB+AD)= 2(9 \sqrt{2}+6 \sqrt{2})=30 \sqrt{2}(\ \mathrm {cm})，$

$面积为AB·DE=9\sqrt{2}×3\sqrt{6}=54\sqrt{3}(\ \mathrm {cm^2}).$