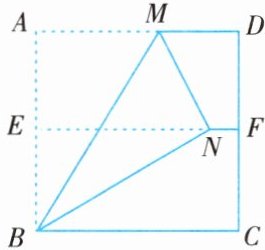
1. 将宣纸按需折叠,确保每一层都压扁压平,这样可以更方便地剪出对称的图案.小悦利用一张正方形宣纸$ABCD$作如下操作:①如图所示,先对折正方形$ABCD$,使$AD$与$BC$重合,得到折痕$EF$,把宣纸展平;②再一次折叠宣纸,使点$A$落在$EF$上的点$N$处,并使折痕经过点$B$,得到折痕$BM$和线段$BN$,$MN$.若线段$BN=6cm$,则线段$EN$的长为(
A. $\sqrt {3}cm$
B. $2\sqrt {3}cm$
C. $\frac {3\sqrt {3}}{2}cm$
D. $3\sqrt {3}cm$
D
)
A. $\sqrt {3}cm$
B. $2\sqrt {3}cm$
C. $\frac {3\sqrt {3}}{2}cm$
D. $3\sqrt {3}cm$
答案:
D
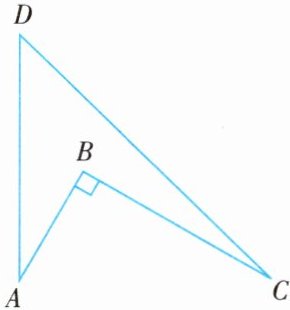
2. 在折叠好的宣纸上用铅笔画出轮廓和细节,确保线条清晰.小悦画出的轮廓部分如图所示,通过相应测量工具测量:已知$∠ABC=90^{\circ },AB=1,BC=\sqrt {3},CD=2\sqrt {2},AD=2$.根据以上信息,请你求出该轮廓的面积.
解: 该轮廓的面积$=S_{\triangle ACD}-S_{\triangle ABC}=\frac {1}{2}AD\cdot AC-\frac {1}{2}AB\cdot BC=$

解: 该轮廓的面积$=S_{\triangle ACD}-S_{\triangle ABC}=\frac {1}{2}AD\cdot AC-\frac {1}{2}AB\cdot BC=$
$2-\frac {\sqrt {3}}{2}$
.
答案:
解: 该轮廓的面积$=S_{\triangle ACD}-S_{\triangle ABC}=\frac {1}{2}AD\cdot AC-\frac {1}{2}AB\cdot BC=2-\frac {\sqrt {3}}{2}$.
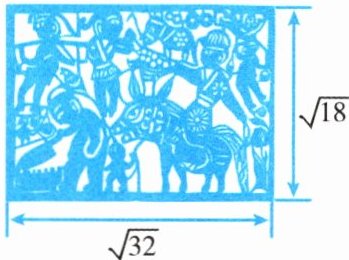
3. 剪好后将宣纸展开,细心贴裱作品,确保作品平整美观.如图所示,这是小悦的参赛作品(单位:$dm$).
(1)通过计算,判断小悦的作品是否符合参赛标准;
(2)妈妈给小悦提出建议:在参赛作品周围贴上金色彩条,这样参赛作品更漂亮,则需要彩条的长度约为多少?(彩条的宽度忽略不计,结果保留一位小数,参考数据:$\sqrt {2}\approx 1.4$)
(1)解: 由题意, 得$\sqrt {18}×\sqrt {32}=$
$\because 24>20$,∴小悦的作品符合参赛标准;
(2)解: 由题意, 得$2(\sqrt {18}+\sqrt {32})=14\sqrt {2}\approx $
∴需要彩条的长度约为 19.6 dm.
(1)通过计算,判断小悦的作品是否符合参赛标准;
(2)妈妈给小悦提出建议:在参赛作品周围贴上金色彩条,这样参赛作品更漂亮,则需要彩条的长度约为多少?(彩条的宽度忽略不计,结果保留一位小数,参考数据:$\sqrt {2}\approx 1.4$)

(1)解: 由题意, 得$\sqrt {18}×\sqrt {32}=$
24
$(dm^{2})$.$\because 24>20$,∴小悦的作品符合参赛标准;
(2)解: 由题意, 得$2(\sqrt {18}+\sqrt {32})=14\sqrt {2}\approx $
19.6
(dm).∴需要彩条的长度约为 19.6 dm.
答案:
解:
(1) 由题意, 得$\sqrt {18}×\sqrt {32}=24(dm^{2})$.
$\because 24>20$,
∴小悦的作品符合参赛标准;
(2) 由题意, 得$2(\sqrt {18}+\sqrt {32})=14\sqrt {2}\approx 19.6$(dm).
∴需要彩条的长度约为 19.6 dm.
(1) 由题意, 得$\sqrt {18}×\sqrt {32}=24(dm^{2})$.
$\because 24>20$,
∴小悦的作品符合参赛标准;
(2) 由题意, 得$2(\sqrt {18}+\sqrt {32})=14\sqrt {2}\approx 19.6$(dm).
∴需要彩条的长度约为 19.6 dm.
查看更多完整答案,请扫码查看


