1. 已知平行四边形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于 $O$。则下列说法正确的是(
A. 当 $OA = OC$ 时,平行四边形 $ABCD$ 为矩形
B. 当 $AB = AD$ 时,平行四边形 $ABCD$ 为正方形
C. 当 $\angle ABC = 90^{\circ}$ 时,平行四边形 $ABCD$ 为菱形
D. 当 $AC\perp BD$ 时,平行四边形 $ABCD$ 为菱形
D
)A. 当 $OA = OC$ 时,平行四边形 $ABCD$ 为矩形
B. 当 $AB = AD$ 时,平行四边形 $ABCD$ 为正方形
C. 当 $\angle ABC = 90^{\circ}$ 时,平行四边形 $ABCD$ 为菱形
D. 当 $AC\perp BD$ 时,平行四边形 $ABCD$ 为菱形
答案:
1.D
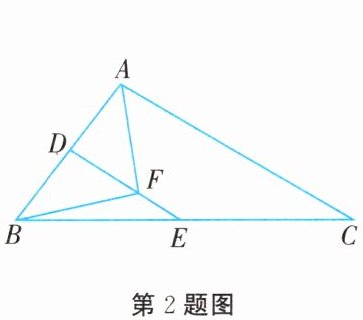
2. 如图所示,在 $\triangle ABC$ 中,$D$,$E$ 分别为 $AB$,$BC$ 的中点,点 $F$ 在 $DE$ 上,且 $AF\perp BF$。若 $AB = 7$,$AC = 12$,则 $EF$ 的长为(
A. 1
B. 1.5
C. 2
D. 2.5
D
)
A. 1
B. 1.5
C. 2
D. 2.5
答案:
2.D
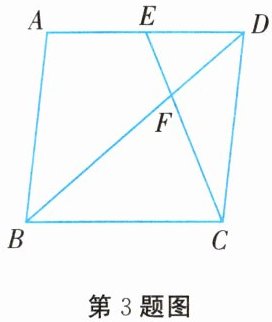
3. 如图所示,在边长为 4 的菱形 $ABCD$ 中,$E$ 为 $AD$ 边的中点,连接 $CE$ 交对角线 $BD$ 于点 $F$。若 $\angle DEF=\angle DFE$,则这个菱形的面积为(
A. 16
B. $6\sqrt{7}$
C. $12\sqrt{7}$
D. 30
B
)
A. 16
B. $6\sqrt{7}$
C. $12\sqrt{7}$
D. 30
答案:
3.B
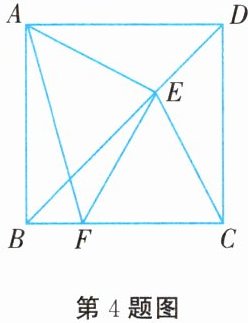
4. 如图所示,点 $E$ 是正方形 $ABCD$ 对角线 $BD$ 上一点,点 $F$ 在 $BC$ 上且 $EF = EC$,连接 $AE$,$AF$。若 $\angle ECF=\alpha$,$\angle AFB=\beta$,则(
A. $\alpha+\beta = 135^{\circ}$
B. $\beta-\alpha = 15^{\circ}$
C. $2\beta-\alpha = 90^{\circ}$
D. $2\alpha+\beta = 180^{\circ}$
A
)
A. $\alpha+\beta = 135^{\circ}$
B. $\beta-\alpha = 15^{\circ}$
C. $2\beta-\alpha = 90^{\circ}$
D. $2\alpha+\beta = 180^{\circ}$
答案:
4.A
5. 在 $\triangle ABC$ 中,$AB = AC$,要将该等腰三角形剪一刀后,再将两部分拼成一个平行四边形,现有图①和图②的两种方案,则正确的方案(
图①甲:
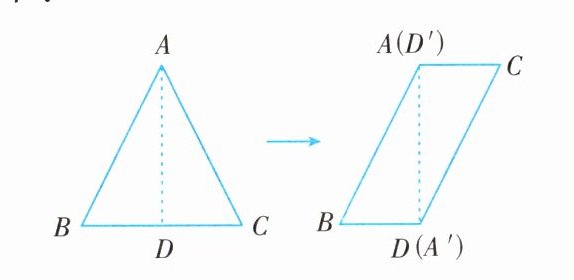
①取 $BC$ 的中点 $D$;
②将 $\triangle ABC$ 沿 $AD$ 剪开;
③将 $A'$,$D'$ 分别与点 $D$,$A$ 重合即可。
图②乙:
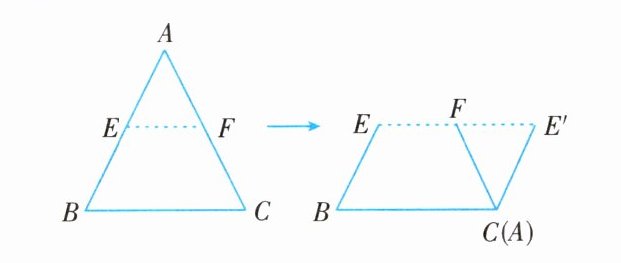
①分别取 $AB$,$AC$ 的中点 $E$,$F$;
②将 $\triangle ABC$ 沿 $EF$ 剪开;
③将 $\triangle AEF$ 绕点 $F$ 顺时针旋转 $180^{\circ}$ 即可。
A. 只有甲方案是
B. 只有乙方案是
C. 甲、乙两个方案都是
D. 甲、乙两个方案都不是
C
)图①甲:

①取 $BC$ 的中点 $D$;
②将 $\triangle ABC$ 沿 $AD$ 剪开;
③将 $A'$,$D'$ 分别与点 $D$,$A$ 重合即可。
图②乙:

①分别取 $AB$,$AC$ 的中点 $E$,$F$;
②将 $\triangle ABC$ 沿 $EF$ 剪开;
③将 $\triangle AEF$ 绕点 $F$ 顺时针旋转 $180^{\circ}$ 即可。
A. 只有甲方案是
B. 只有乙方案是
C. 甲、乙两个方案都是
D. 甲、乙两个方案都不是
答案:
5.C
查看更多完整答案,请扫码查看


