9. 如图所示是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:$AM = 4\ \text{m}$,$AB = 8\ \text{m}$,$\angle MAD = 45^{\circ}$,$\angle MBC = 30^{\circ}$,则警示牌的高$CD$为______
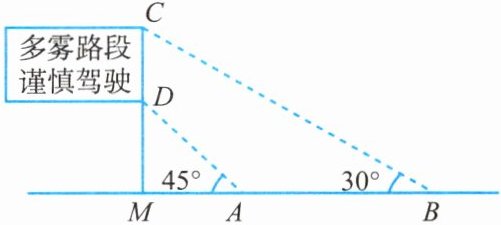
2.9
$\text{m}$(结果精确到$0.1\ \text{m}$,参考数据:$\sqrt{2}\approx1.41$,$\sqrt{3}\approx1.73$).
答案:
9.2.9
10. 阅读:在平面直角坐标系中,已知两点的坐标,可构造直角三角形,运用勾股定理,求这两点间的距离.在平面直角坐标系中有两点$A(-3,5)$,$B(1,2)$,求$A$,$B$两点间的距离.
如图1所示,过点$A$作$x$轴的垂线,过点$B$作$y$轴的垂线,相交于点$C$,连接$AB$.
$\therefore AC = |5 - 2| = 3$,$BC = |1 - (-3)| = 4$.
在$\text{Rt}\triangle ABC$中,由勾股定理得:$AB =\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$.
若$M(x_{1},y_{1})$,$N(x_{2},y_{2})$,从而得到两点间的距离公式$MN =\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$.
解决下列问题:
(1)若$P(2,4)$,$Q(-3,-8)$,则$PQ$两点之间的距离$PQ =$______;
(2)如图2所示,已知点$D(3,3)$,$E(5,-1)$,若$OH\perp DE$,则$OH$的长是多少?
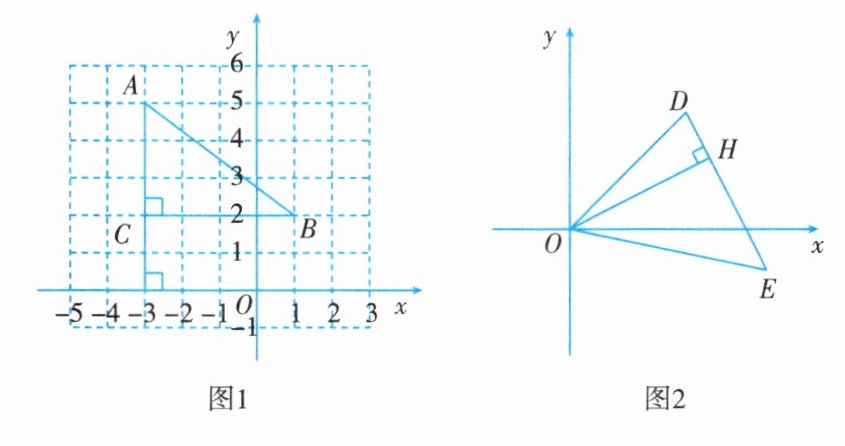
如图1所示,过点$A$作$x$轴的垂线,过点$B$作$y$轴的垂线,相交于点$C$,连接$AB$.
$\therefore AC = |5 - 2| = 3$,$BC = |1 - (-3)| = 4$.
在$\text{Rt}\triangle ABC$中,由勾股定理得:$AB =\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$.
若$M(x_{1},y_{1})$,$N(x_{2},y_{2})$,从而得到两点间的距离公式$MN =\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}$.
解决下列问题:
(1)若$P(2,4)$,$Q(-3,-8)$,则$PQ$两点之间的距离$PQ =$______;
(2)如图2所示,已知点$D(3,3)$,$E(5,-1)$,若$OH\perp DE$,则$OH$的长是多少?

答案:
解:
(1)13
(2)
∵点D(3,3),E(5,−1),
∴DE=$\sqrt{(5−3)^2+(−1−3)^2}$=2$\sqrt{5}$。
如图所示,过点D作DA⊥y轴于点A,过点E作EC⊥y轴于点C,过点E作EB⊥AD的延长线于点B。
∴四边形ABEC是矩形。
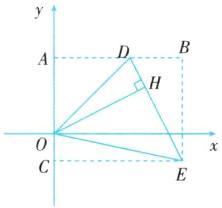
∵D(3,3),E(5,−1),
∴AC=BE=3−(−1)=4,AB=CE=5,AD=3,DB=5−3=2,OA=3,OC=1。
∴S△ODE=S矩形ABEC−S△AOD−S△BDE−S△COE=20−$\frac{9}{2}$−4−$\frac{5}{2}$=9。
∵S△ODE=$\frac{1}{2}$DE·OH,
∴OH=$\frac{2S_{\triangle ODE}}{DE}$=$\frac{2×9}{2\sqrt{5}}$=$\frac{9\sqrt{5}}{5}$。
解:
(1)13
(2)
∵点D(3,3),E(5,−1),
∴DE=$\sqrt{(5−3)^2+(−1−3)^2}$=2$\sqrt{5}$。
如图所示,过点D作DA⊥y轴于点A,过点E作EC⊥y轴于点C,过点E作EB⊥AD的延长线于点B。
∴四边形ABEC是矩形。

∵D(3,3),E(5,−1),
∴AC=BE=3−(−1)=4,AB=CE=5,AD=3,DB=5−3=2,OA=3,OC=1。
∴S△ODE=S矩形ABEC−S△AOD−S△BDE−S△COE=20−$\frac{9}{2}$−4−$\frac{5}{2}$=9。
∵S△ODE=$\frac{1}{2}$DE·OH,
∴OH=$\frac{2S_{\triangle ODE}}{DE}$=$\frac{2×9}{2\sqrt{5}}$=$\frac{9\sqrt{5}}{5}$。
11. 某勘测队按实际需要构建了平面直角坐标系,并标示了$A$,$B$,$C$三地的坐标,数据如图所示(单位:$\text{km}$).笔直铁路经过$A$,$B$两地.
(1)$A$,$B$间的距离为______$\text{km}$;
(2)计划修一条从$C$到铁路$AB$的最短公路$l$,并在$l$上建一个维修站$D$,使$D$到$A$,$C$的距离相等,求$C$,$D$间的距离.
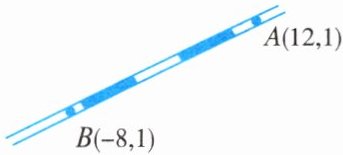
(1)$A$,$B$间的距离为______$\text{km}$;
(2)计划修一条从$C$到铁路$AB$的最短公路$l$,并在$l$上建一个维修站$D$,使$D$到$A$,$C$的距离相等,求$C$,$D$间的距离.

答案:
解:
(1)20
(2)如图所示,过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交l于点D,连接AD。

易知CE=1−(−17)=18,AE=12,设CD=x,则AD=CD=x。
由勾股定理,可知x²=(18−x)²+12²,解得x=13。
答:C,D间的距离为13千米。
解:
(1)20
(2)如图所示,过点C作l⊥AB于点E,连接AC,作AC的垂直平分线交l于点D,连接AD。

易知CE=1−(−17)=18,AE=12,设CD=x,则AD=CD=x。
由勾股定理,可知x²=(18−x)²+12²,解得x=13。
答:C,D间的距离为13千米。
查看更多完整答案,请扫码查看


