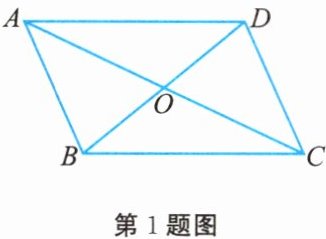
1. 如图所示,$□ ABCD$的对角线交于点$O$,且$AB = 5$,$\triangle OCD$的周长为$23$,则$□ ABCD$的两条对角线的和是(
A. 18
B. 28
C. 36
D. 46
C
)
A. 18
B. 28
C. 36
D. 46
答案:
C
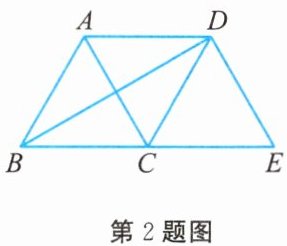
2. 如图所示,将等边三角形$ABC$沿射线$BC$向右平移到$\triangle DCE$的位置,连接$AD$,$BD$,则下列结论:①$AD = BC$;②$BD$,$AC$互相平分;③四边形$ACED$是菱形. 其中正确的有(
A. 0 个
B. 1 个
C. 2 个
D. 3 个
D
)
A. 0 个
B. 1 个
C. 2 个
D. 3 个
答案:
D
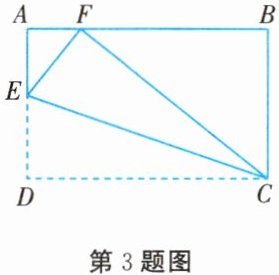
3. 如图所示,在矩形$ABCD$纸片中,$E$为$AD$上一点,将$\triangle CDE$沿$CE$翻折至$\triangle CFE$. 若点$F$恰好落在$AB$上,$AF = 4$,$BC = 10$,则$DE=$(
A. 5.8
B. 5
C. 4.8
D. 3
A
)
A. 5.8
B. 5
C. 4.8
D. 3
答案:
A
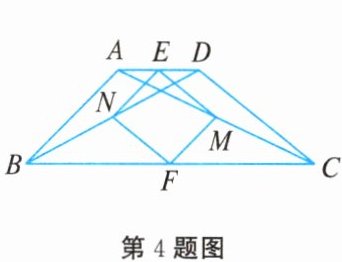
4. 如图所示,$AC$,$BD$是四边形$ABCD$的对角线,点$E$,$F$分别是$AD$,$BC$的中点,点$M$,$N$分别是$AC$,$BD$的中点,连接$EM$,$MF$,$FN$,$NE$,要使四边形$EMFN$为正方形,则需添加的条件是(
A. $AB = DC$,$AB\perp DC$
B. $AB = DC$,$AD = BC$
C. $AB = DC$,$AC\perp DB$
D. $AB = DC$,$AD// BC$
A
)
A. $AB = DC$,$AB\perp DC$
B. $AB = DC$,$AD = BC$
C. $AB = DC$,$AC\perp DB$
D. $AB = DC$,$AD// BC$
答案:
A
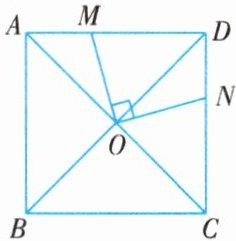
5. 如图所示,正方形$ABCD$的对角线$AC$,$BD$相交于点$O$,$M$是$AD$上的一点,连接$OM$,过点$O$作$ON\perp OM$,交$CD$于点$N$. 若四边形$MOND$的面积是$3$,则$AB$的长为(
A. $\sqrt{2}$
B. $\sqrt{3}$
C. $2\sqrt{2}$
D. $2\sqrt{3}$
D
)
A. $\sqrt{2}$
B. $\sqrt{3}$
C. $2\sqrt{2}$
D. $2\sqrt{3}$
答案:
D
6. 下列图形都是由同样大小的矩形按一定的规律组成,其中第(1)个图形的面积为$2\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$,第(2)个图形的面积为$8\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$,第(3)个图形的面积为$18\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$,$\cdots$,则第(10)个图形的面积为(

A. $196\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
B. $200\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
C. $216\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
D. $256\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
B
)
A. $196\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
B. $200\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
C. $216\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
D. $256\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$
答案:
B
查看更多完整答案,请扫码查看


