8. 农科院助农团队在某地各选6块试验田试种甲、乙两种杂交水稻,收获后统计结果为:$\overline{x}_{甲}=1530.76$千克/亩,$s^{2}_{甲}=6.5$,$\overline{x}_{乙}=1530.76$千克/亩,$s^{2}_{乙}=1.2$,则
乙
(选填“甲”或“乙”)品种更适合在该地区推广.
答案:
8. 乙
9. 如图所示,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 3$,$BC = 1$,边$AC$在数轴上,以点$A$为圆心,$AB$长为半径画弧,交数轴于点$D$,则点$D$表示的数是
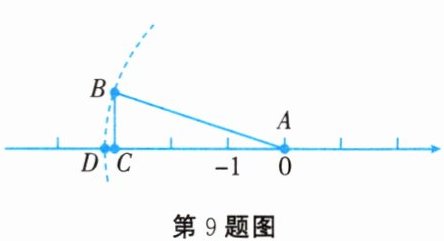
$-\sqrt{10}$
.
答案:
9. $-\sqrt{10}$
10. 一副三角板按如图所示放置,点$C$在$FD$的延长线上,$AB// CF$,$\angle F=\angle ACB = 90^{\circ}$,$\angle E = 45^{\circ}$,$\angle A = 60^{\circ}$. 若$AB = DE = 8$,则$BE =$
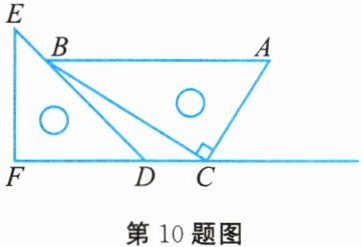
$8 - 2\sqrt{6}$
(结果保留根号).
答案:
10. $8 - 2\sqrt{6}$
11. 在平面直角坐标系中,点$A$,$B$,$C$的坐标分别是$A(0,1)$,$B(1,0)$,$C(3,1)$,点$D$是$x$轴上的点. 如果以$A$,$B$,$C$,$D$为顶点的四边形是平行四边形,那么点$D$的坐标是
$(4,0)$或$(-2,0)$
.
答案:
11. $(4,0)$或$(-2,0)$
12. 某居民小区有块形状为矩形$ABCD$的绿地,长$BC$为$\sqrt{128}$米,宽$AB$为$\sqrt{50}$米. 现在要在矩形绿地中修建两个形状大小相同的长方形花坛(即图中阴影部分),每个长方形花坛的长为$(\sqrt{13}+1)$米,宽为$(\sqrt{13}-1)$米.
(1)求矩形$ABCD$的周长;(结果化为最简二次根式)
(2)除去修建花坛的地方,其他地方全修建成通道,通道上要铺上造价为$6$元/平方米的地砖,要铺完整个通道,则购买地砖至少需要花费多少元?

(1)求矩形$ABCD$的周长;(结果化为最简二次根式)
$26\sqrt{2}$米
(2)除去修建花坛的地方,其他地方全修建成通道,通道上要铺上造价为$6$元/平方米的地砖,要铺完整个通道,则购买地砖至少需要花费多少元?
336

答案:
12. 解:
(1)
∵矩形ABCD的长BC为 $\sqrt{128}$米,宽AB为 $\sqrt{50}$米,
∴$C_{矩形ABCD}=2×( \sqrt{128}+ \sqrt{50})=2× (8 \sqrt{2}+5 \sqrt{2})=26 \sqrt{2}$(米).
(2)通道的面积为$\sqrt{128}×\sqrt{50} - 2(\sqrt{13} + 1)(\sqrt{13} - 1) = 56$(平方米),购买地砖需要花费$56×6 = 336$(元).
(1)
∵矩形ABCD的长BC为 $\sqrt{128}$米,宽AB为 $\sqrt{50}$米,
∴$C_{矩形ABCD}=2×( \sqrt{128}+ \sqrt{50})=2× (8 \sqrt{2}+5 \sqrt{2})=26 \sqrt{2}$(米).
答:矩形ABCD的周长为$26 \sqrt{2}$米.
(2)通道的面积为$\sqrt{128}×\sqrt{50} - 2(\sqrt{13} + 1)(\sqrt{13} - 1) = 56$(平方米),购买地砖需要花费$56×6 = 336$(元).
13. 如图所示,在平行四边形$ABCD$中,$E$为线段$AD$的中点,$BE$与$CD$的延长线交于点$F$,连接$AF$,$BD$,$\angle BDF = 90^{\circ}$.
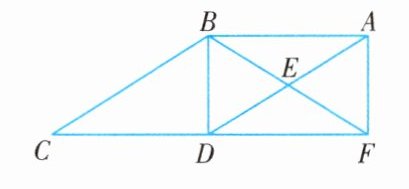
(1)求证:四边形$ABDF$是矩形;
证明:∵四边形ABCD是平行四边形,∴AB//DC,即AB//FD.∴∠ABF=∠BFD,∠BAD=∠ADF.∵E为线段AD的中点,∴AE=DE.在△ABE与△DFE中,$\begin{cases}{∠ABE=∠DFE}\\{∠BAE=∠FDE}\\{AE=DE}\end{cases}$∴△ABE≌△DFE(AAS).∴BE=EF.∵四边形ABDF是平行四边形,∠BDF=90°,∴四边形ABDF是矩形.
(2)若$BC = 4$,$DF = 3$,求四边形$ABCF$的面积$S$.
解:∵四边形$ABCD$是平行四边形,∴$BC = AD$.∵四边形$ABDF$是矩形,∴$AD = BF$.∴$BC = BF = 4$.∵$BD⊥CF$,$CD = DF = 3$,∴$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{4^{2} - 3^{2}} = \sqrt{7}$.∴$S_{四边形ABCF} = S_{\triangle BCD} + S_{矩形ABDF} = $

(1)求证:四边形$ABDF$是矩形;
证明:∵四边形ABCD是平行四边形,∴AB//DC,即AB//FD.∴∠ABF=∠BFD,∠BAD=∠ADF.∵E为线段AD的中点,∴AE=DE.在△ABE与△DFE中,$\begin{cases}{∠ABE=∠DFE}\\{∠BAE=∠FDE}\\{AE=DE}\end{cases}$∴△ABE≌△DFE(AAS).∴BE=EF.∵四边形ABDF是平行四边形,∠BDF=90°,∴四边形ABDF是矩形.
(2)若$BC = 4$,$DF = 3$,求四边形$ABCF$的面积$S$.
解:∵四边形$ABCD$是平行四边形,∴$BC = AD$.∵四边形$ABDF$是矩形,∴$AD = BF$.∴$BC = BF = 4$.∵$BD⊥CF$,$CD = DF = 3$,∴$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{4^{2} - 3^{2}} = \sqrt{7}$.∴$S_{四边形ABCF} = S_{\triangle BCD} + S_{矩形ABDF} = $
$\frac{9\sqrt{7}}{2}$
.
答案:
13.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//DC,即AB//FD.
∴∠ABF=∠BFD,∠BAD=∠ADF.
∵E为线段AD的中点,
∴AE=DE.
∴△ABE≌△DFE(AAS).
∴BE=EF.
∴四边形ABCD是平行四边形
∵∠BDF=90°,
∴四边形ABDF是矩形.
(2)解:
∵四边形$ABCD$是平行四边形,
∴$BC = AD$.
∵四边形$ABDF$是矩形,
∴$AD = BF$.
∴$BC = BF = 4$.
∵$BD⊥CF$,$CD = DF = 3$,
∴$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{4^{2} - 3^{2}} = \sqrt{7}$.
∴$S_{四边形ABCF} = S_{\triangle BCD} + S_{矩形ABDF} = \frac{9\sqrt{7}}{2}$.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//DC,即AB//FD.
∴∠ABF=∠BFD,∠BAD=∠ADF.
∵E为线段AD的中点,
∴AE=DE.
在△ABE与△DFE中,
$\begin{cases}{∠ABE=∠DFE}\\{∠BAE=∠FDE}\\{AE=DE}\end{cases}$
∴△ABE≌△DFE(AAS).
∴BE=EF.
∴四边形ABCD是平行四边形
∵∠BDF=90°,
∴四边形ABDF是矩形.
(2)解:
∵四边形$ABCD$是平行四边形,
∴$BC = AD$.
∵四边形$ABDF$是矩形,
∴$AD = BF$.
∴$BC = BF = 4$.
∵$BD⊥CF$,$CD = DF = 3$,
∴$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{4^{2} - 3^{2}} = \sqrt{7}$.
∴$S_{四边形ABCF} = S_{\triangle BCD} + S_{矩形ABDF} = \frac{9\sqrt{7}}{2}$.
查看更多完整答案,请扫码查看


