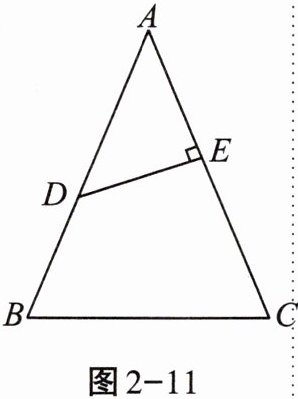
3. 如图2-11,在$\triangle ABC$中,$AB = AC = 13$,$BC = 10$,$D是AB$的中点,过点$D作DE\perp AC$,垂足为$E$,则$DE$的长是______.

答案:
$\frac{60}{13}$ 解析:如答图2-2,作$AH\perp BC$,垂足为$H$,连接$CD$,

在$Rt\triangle ABH$中,$AH=\sqrt{13^{2}-5^{2}} = 12$,
$\therefore S_{\triangle ABC}=\frac{1}{2}×10×12 = 60$.
$\because D$为$AB$的中点,$\therefore S_{\triangle ADC}=S_{\triangle DBC}=30$,
$\therefore \frac{1}{2}\cdot AC\cdot DE = 30$,即$DE=\frac{60}{13}$.
$\frac{60}{13}$ 解析:如答图2-2,作$AH\perp BC$,垂足为$H$,连接$CD$,

在$Rt\triangle ABH$中,$AH=\sqrt{13^{2}-5^{2}} = 12$,
$\therefore S_{\triangle ABC}=\frac{1}{2}×10×12 = 60$.
$\because D$为$AB$的中点,$\therefore S_{\triangle ADC}=S_{\triangle DBC}=30$,
$\therefore \frac{1}{2}\cdot AC\cdot DE = 30$,即$DE=\frac{60}{13}$.
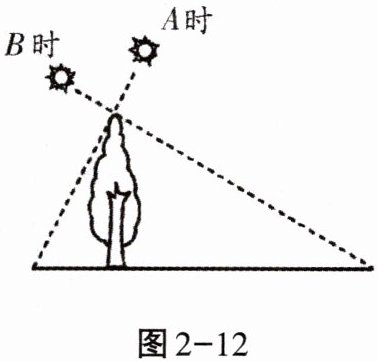
4. 如图2-12,小明在$A$时测得某树的影长为2m,$B$时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为______m.

答案:
解析:如答图2-3,$EH = 2$,$FH = 8$,$DH\perp EF$,$ED\perp DF$,

设$DH = x$,则由$DE^{2}+DF^{2}=EF^{2}$,
得$x^{2}+2^{2}+x^{2}+8^{2}=(2 + 8)^{2}$,解得$x = 4$.
解析:如答图2-3,$EH = 2$,$FH = 8$,$DH\perp EF$,$ED\perp DF$,

设$DH = x$,则由$DE^{2}+DF^{2}=EF^{2}$,
得$x^{2}+2^{2}+x^{2}+8^{2}=(2 + 8)^{2}$,解得$x = 4$.
5. 公园里有一块四边形$ABCD$的草地如图2-13所示,测得$BC = CD = 10m$,$\angle B = \angle C = 120^{\circ}$,$\angle A = 45^{\circ}$.请你求出这块草地的面积.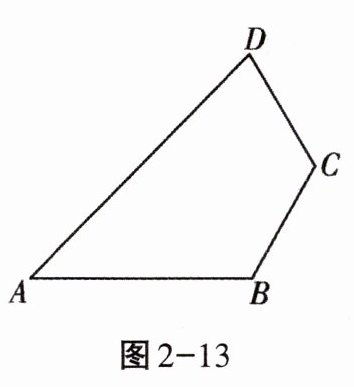

答案:
解:如答图2-4,连接$DB$,$\because DC = BC$,$\angle C = 120^{\circ}$,$\therefore \angle 1 = 30^{\circ}$,
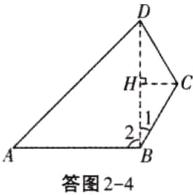
$\therefore \angle 2 = 120^{\circ}-30^{\circ}=90^{\circ}$.作$CH\perp DB$,垂足为$H$,
在$Rt\triangle CHB$中,$CH = 5$,$HB = 5\sqrt{3}$,$AB = DB = 10\sqrt{3}$,
$\therefore S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BDC}=\frac{1}{2}×(10\sqrt{3})^{2}+\frac{1}{2}×10\sqrt{3}×5=(150 + 25\sqrt{3})(m^{2})$.
解:如答图2-4,连接$DB$,$\because DC = BC$,$\angle C = 120^{\circ}$,$\therefore \angle 1 = 30^{\circ}$,

$\therefore \angle 2 = 120^{\circ}-30^{\circ}=90^{\circ}$.作$CH\perp DB$,垂足为$H$,
在$Rt\triangle CHB$中,$CH = 5$,$HB = 5\sqrt{3}$,$AB = DB = 10\sqrt{3}$,
$\therefore S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BDC}=\frac{1}{2}×(10\sqrt{3})^{2}+\frac{1}{2}×10\sqrt{3}×5=(150 + 25\sqrt{3})(m^{2})$.
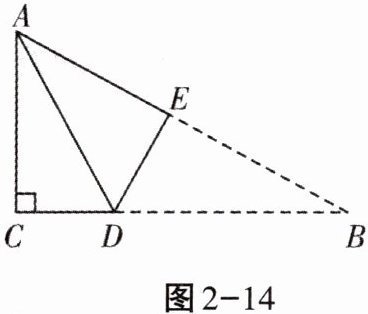
1. 如图2-14,有一张直角三角形纸片,两直角边$AC = 5cm$,$BC = 10cm$,将$\triangle ABC$折叠,使点$B与点A$重合,折痕为$DE$,则$CD$的长为( )
A.$\frac{25}{2}cm$
B.$\frac{15}{2}cm$
C.$\frac{25}{4}cm$
D.$\frac{15}{4}cm$

A.$\frac{25}{2}cm$
B.$\frac{15}{2}cm$
C.$\frac{25}{4}cm$
D.$\frac{15}{4}cm$
答案:
D 解析:如答图2-5,

$\because AE = EB$,$DE\perp AB$,$\therefore AD = DB$.
设$CD = x$,则$AD = BD = 10 - x$.
在$Rt\triangle ACD$中,$(10 - x)^{2}=x^{2}+5^{2}$,
解得$x=\frac{15}{4}$,$\therefore CD=\frac{15}{4}cm$.
D 解析:如答图2-5,

$\because AE = EB$,$DE\perp AB$,$\therefore AD = DB$.
设$CD = x$,则$AD = BD = 10 - x$.
在$Rt\triangle ACD$中,$(10 - x)^{2}=x^{2}+5^{2}$,
解得$x=\frac{15}{4}$,$\therefore CD=\frac{15}{4}cm$.
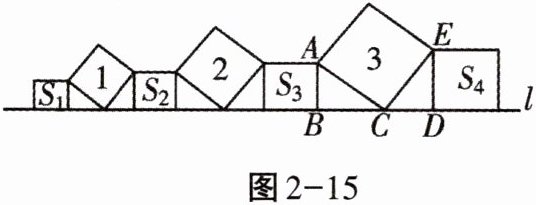
2. 在直线$l$上依次摆放着7个正方形(如图2-15).已知斜放置的3个正方形的面积分别是1,2,3,正放置的4个正方形的面积依次是$S_{1}$,$S_{2}$,$S_{3}$,$S_{4}$,试求$S_{1} + S_{2} + S_{3} + S_{4}$的值.

4
答案:
解:$\because \angle BAC+\angle ACB=\angle ACB+\angle ECD = 90^{\circ}$,
$\therefore \angle BAC=\angle ECD$,又$\because \angle ABC=\angle CDE = 90^{\circ}$,$AC = CE$,
$\therefore \triangle ABC\cong\triangle CDE$,
$\therefore AB = CD$,$BC = ED$,
$\therefore AC^{2}=3 = AB^{2}+BC^{2}=S_{3}+S_{4}$,即$S_{3}+S_{4}=3$.
同理,$2 = S_{2}+S_{3}$,$S_{1}+S_{2}=1$,$\therefore S_{1}+S_{2}+S_{3}+S_{4}=1 + 3 = 4$.
$\therefore \angle BAC=\angle ECD$,又$\because \angle ABC=\angle CDE = 90^{\circ}$,$AC = CE$,
$\therefore \triangle ABC\cong\triangle CDE$,
$\therefore AB = CD$,$BC = ED$,
$\therefore AC^{2}=3 = AB^{2}+BC^{2}=S_{3}+S_{4}$,即$S_{3}+S_{4}=3$.
同理,$2 = S_{2}+S_{3}$,$S_{1}+S_{2}=1$,$\therefore S_{1}+S_{2}+S_{3}+S_{4}=1 + 3 = 4$.
查看更多完整答案,请扫码查看


