《2025年暑假作业兰州大学出版社八年级数学人教版》

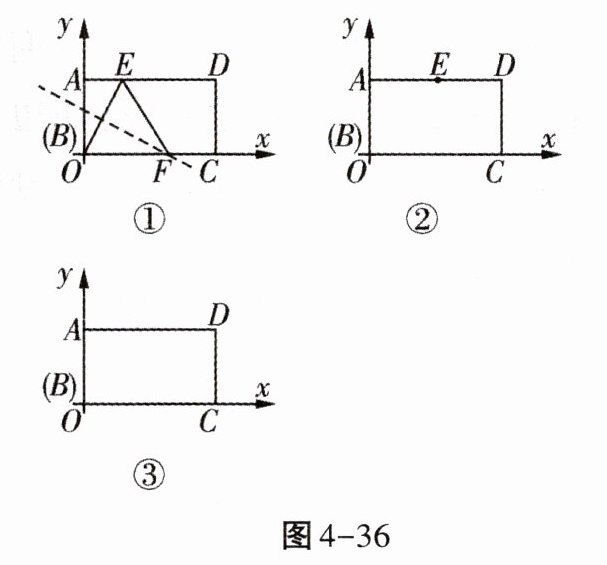
如图4-36①,在矩形ABCD中,将矩形折叠,使B落在边AD(含端点)上,落点记为E,这时折痕与边BC或者边CD(含端点)交于F,然后展开铺平,则以B,E,F为顶点的△BEF称为矩形ABCD的“折痕三角形”.

(1)由“折痕三角形”的定义可知,矩形ABCD的任意一个“折痕△BEF”是一个______三角形；
(2)如图4-36②,在矩形ABCD中,AB= 2,BC= 4,当它的“折痕△BEF”的顶点E位于AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标；
(3)如图4-36③,在矩形ABCD中,AB= 2,BC= 4,该矩形是否存在面积最大的“折痕△BEF”？若存在,说明理由,并求出此时点E的坐标；若不存在,为什么？

答案：
解:
(1)等腰
(2)如答图4-4①,连接$BE$,作$BE$的垂直平分线交$BC$于点$F$,连接$EF$,$\triangle BEF$是矩形$ABCD$的一个折痕三角形.$\because$折痕垂直平分$BE$,$AB=AE=2$,
　　$\therefore$点$A$在$BE$的垂直平分线上，即折痕经过点$A$，
　　$\therefore$四边形$ABFE$为正方形,$\therefore BF=AB=2$,
　　$\therefore F$的坐标为$(2,0)$.
(3)矩形$ABCD$存在面积最大的折痕$\triangle BEF$,其面积为4.
　　理由如下:①当$F$在边$BC$上时,如答图4-7②所示,
　　　$S_{\triangle BEF}\leq \frac{1}{2}S_{矩形ABCD}$,
即当$F$与$C$重合时，$\triangle BEF$的面积最大为4.
　　②当$F$在边$CD$上时，如答图4-4③所示，
　　过$F$作$FH// BC$交$AB$于点$H$,交$BE$于点$K$,
　　$\because S_{\triangle EKF}=\frac{1}{2}KF\cdot AH\leq \frac{1}{2}HF\cdot AH=\frac{1}{2}S_{矩形AHFD}$,
　　$S_{\triangle BKF}=\frac{1}{2}KF\cdot BH\leq \frac{1}{2}HF\cdot BH=\frac{1}{2}S_{矩形BCFH}$,
　　$\therefore S_{\triangle BEF}\leq \frac{1}{2}S_{矩形ABCD}=4$,
　　即当$F$为$CD$的中点时，
　　$\triangle BEF$的面积最大为4.
　　下面求面积最大时，点$E$的坐标:
　　①当$F$与点$C$重合时,如答图4-4④所示,
　　由折叠可知$CE=CB=4$,
　　在$Rt\triangle CDE$中,$ED=\sqrt{CE^{2}-CD^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$,
　　$\therefore AE=4-2\sqrt{3}$,$\therefore E$的坐标为$(4-2\sqrt{3},2)$.
　　②当$F$在边$DC$的中点时，点$E$与点$A$重合,如答图4-4⑤所示，此时$E$的坐标为$(0,2)$.
　　综上所述，折痕$\triangle BEF$的最大面积为4时，点$E$的坐标为$(0,2)$或$(4-2\sqrt{3},2)$.