19. (8分)小东在学习了$\frac{\sqrt{a}}{\sqrt{b}}= \sqrt{\frac{a}{b}}$后,认为$\sqrt{\frac{a}{b}}= \frac{\sqrt{a}}{\sqrt{b}}$也成立,因此他认为下面的化简过程是正确的.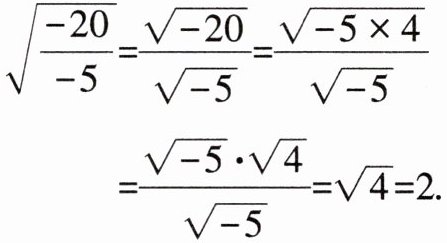
(1)你认为他的化简对吗? 如果对,请说明理由;如果不对,应怎么化简?
(2)说明$\sqrt{\frac{a}{b}}= \frac{\sqrt{a}}{\sqrt{b}}$成立的条件.
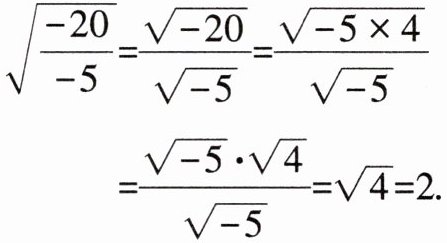
(1)你认为他的化简对吗? 如果对,请说明理由;如果不对,应怎么化简?
不对,正确化简为$\sqrt{\frac{-20}{-5}}=\sqrt{4} = 2$
(2)说明$\sqrt{\frac{a}{b}}= \frac{\sqrt{a}}{\sqrt{b}}$成立的条件.
$a\geqslant0$,$b > 0$
答案:
【解析】:
(1) 他的化简不对。因为在实数范围内,二次根式中被开方数须是非负数,$\sqrt{-20}$,$\sqrt{-5}$无意义。
正确化简:$\sqrt{\frac{-20}{-5}}=\sqrt{4} = 2$。
(2) 对于$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$,根据二次根式的性质,根号下的数须非负,且分母不能为$0$,所以$a\geqslant0$,$b > 0$。
【答案】:
(1) 不对,正确化简为$\sqrt{\frac{-20}{-5}}=\sqrt{4} = 2$;
(2) $a\geqslant0$,$b > 0$。
(1) 他的化简不对。因为在实数范围内,二次根式中被开方数须是非负数,$\sqrt{-20}$,$\sqrt{-5}$无意义。
正确化简:$\sqrt{\frac{-20}{-5}}=\sqrt{4} = 2$。
(2) 对于$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$,根据二次根式的性质,根号下的数须非负,且分母不能为$0$,所以$a\geqslant0$,$b > 0$。
【答案】:
(1) 不对,正确化简为$\sqrt{\frac{-20}{-5}}=\sqrt{4} = 2$;
(2) $a\geqslant0$,$b > 0$。
20. (8分)先化简,再求值:
(1)$\left(a - 1 + \frac{2}{a + 1}\right)÷(a^2+1)$,其中$a= \sqrt{2}-1$;
(2)$(x+1)^2-x(x+2y)-2x$,其中$x= \sqrt{3}+1$,$y= \sqrt{3}-1$.
(1)$\left(a - 1 + \frac{2}{a + 1}\right)÷(a^2+1)$,其中$a= \sqrt{2}-1$;
$\frac{\sqrt{2}}{2}$
(2)$(x+1)^2-x(x+2y)-2x$,其中$x= \sqrt{3}+1$,$y= \sqrt{3}-1$.
$-3$
答案:
【解析】:
(1)
先化简$\left(a - 1+\frac{2}{a + 1}\right)÷(a^{2}+1)$:
$\begin{aligned}&\left(a - 1+\frac{2}{a + 1}\right)÷(a^{2}+1)\\=&\left[\frac{(a - 1)(a + 1)}{a + 1}+\frac{2}{a + 1}\right]÷(a^{2}+1)\\=&\left(\frac{a^{2}-1 + 2}{a + 1}\right)÷(a^{2}+1)\\=&\frac{a^{2}+1}{a + 1}×\frac{1}{a^{2}+1}\\=&\frac{1}{a + 1}\end{aligned}$
当$a=\sqrt{2}-1$时,代入$\frac{1}{a + 1}$可得:
$\frac{1}{\sqrt{2}-1 + 1}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$
(2)
先化简$(x + 1)^{2}-x(x + 2y)-2x$:
$\begin{aligned}&(x + 1)^{2}-x(x + 2y)-2x\\=&x^{2}+2x + 1-x^{2}-2xy-2x\\=&1-2xy\end{aligned}$
当$x=\sqrt{3}+1$,$y=\sqrt{3}-1$时,代入$1-2xy$可得:
$\begin{aligned}&1-2×(\sqrt{3}+1)×(\sqrt{3}-1)\\=&1-2×[(\sqrt{3})^{2}-1^{2}]\\=&1-2×(3 - 1)\\=&1-2×2\\=&1 - 4\\=&-3\end{aligned}$
【答案】:
(1)$\frac{\sqrt{2}}{2}$;
(2)$-3$
(1)
先化简$\left(a - 1+\frac{2}{a + 1}\right)÷(a^{2}+1)$:
$\begin{aligned}&\left(a - 1+\frac{2}{a + 1}\right)÷(a^{2}+1)\\=&\left[\frac{(a - 1)(a + 1)}{a + 1}+\frac{2}{a + 1}\right]÷(a^{2}+1)\\=&\left(\frac{a^{2}-1 + 2}{a + 1}\right)÷(a^{2}+1)\\=&\frac{a^{2}+1}{a + 1}×\frac{1}{a^{2}+1}\\=&\frac{1}{a + 1}\end{aligned}$
当$a=\sqrt{2}-1$时,代入$\frac{1}{a + 1}$可得:
$\frac{1}{\sqrt{2}-1 + 1}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$
(2)
先化简$(x + 1)^{2}-x(x + 2y)-2x$:
$\begin{aligned}&(x + 1)^{2}-x(x + 2y)-2x\\=&x^{2}+2x + 1-x^{2}-2xy-2x\\=&1-2xy\end{aligned}$
当$x=\sqrt{3}+1$,$y=\sqrt{3}-1$时,代入$1-2xy$可得:
$\begin{aligned}&1-2×(\sqrt{3}+1)×(\sqrt{3}-1)\\=&1-2×[(\sqrt{3})^{2}-1^{2}]\\=&1-2×(3 - 1)\\=&1-2×2\\=&1 - 4\\=&-3\end{aligned}$
【答案】:
(1)$\frac{\sqrt{2}}{2}$;
(2)$-3$
21. (10分)小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如$3 + 2\sqrt{2} = (1 + \sqrt{2})^2$.善于思考的小明进行了以下探索:
设$a + b\sqrt{2} = (m + n\sqrt{2})^2$(其中$a、b、m、n$均为整数),则有$a + b\sqrt{2} = m^2 + 2n^2 + 2\sqrt{2}mn$.
$\therefore a = m^2 + 2n^2,b = 2mn$. 这样小明就找到了一种把类似$a + b\sqrt{2}$的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:($a,b,m,n$均为正整数)
(1)$a + b\sqrt{3} = (m + n\sqrt{3})^2$,用含$m,n的式子分别表示a,b$,得:$a=$
(2)当$a= 7,n= 1$时,填空:$7+$
(3)若$a + 6\sqrt{3} = (m + n\sqrt{3})^2$,求$a$的值.
设$a + b\sqrt{2} = (m + n\sqrt{2})^2$(其中$a、b、m、n$均为整数),则有$a + b\sqrt{2} = m^2 + 2n^2 + 2\sqrt{2}mn$.
$\therefore a = m^2 + 2n^2,b = 2mn$. 这样小明就找到了一种把类似$a + b\sqrt{2}$的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:($a,b,m,n$均为正整数)
(1)$a + b\sqrt{3} = (m + n\sqrt{3})^2$,用含$m,n的式子分别表示a,b$,得:$a=$
$m^{2}+3n^{2}$
,$b=$$2mn$
;(2)当$a= 7,n= 1$时,填空:$7+$
4
$\sqrt{3}=$(2
$+\sqrt{3})^2$(3)若$a + 6\sqrt{3} = (m + n\sqrt{3})^2$,求$a$的值.
12或28
答案:
【解析】:
(1)
已知$a + b\sqrt{3}=(m + n\sqrt{3})^2$,根据完全平方公式$(A + B)^2=A^{2}+2AB + B^{2}$,将$(m + n\sqrt{3})^2$展开可得:
$(m + n\sqrt{3})^2=m^{2}+2× m× n\sqrt{3}+(n\sqrt{3})^{2}=m^{2}+2mn\sqrt{3}+3n^{2}$。
因为$a + b\sqrt{3}=m^{2}+3n^{2}+2mn\sqrt{3}$,所以$a = m^{2}+3n^{2}$,$b = 2mn$。
(2)
当$a = 7$,$n = 1$时,由$a=m^{2}+3n^{2}$可得:
$7=m^{2}+3×1^{2}$,即$m^{2}+3 = 7$,移项可得$m^{2}=7 - 3=4$,因为$m$为正整数,所以$m = 2$。
由$b = 2mn$,把$m = 2$,$n = 1$代入可得$b=2×2×1 = 4$。
所以$7 + 4\sqrt{3}=(2+\sqrt{3})^2$。
(3)
因为$a + 6\sqrt{3}=(m + n\sqrt{3})^2=m^{2}+3n^{2}+2mn\sqrt{3}$,所以$b = 2mn=6$,则$mn = 3$。
因为$m$,$n$均为正整数,所以有两种情况:
当$m = 1$,$n = 3$时,$a=m^{2}+3n^{2}=1^{2}+3×3^{2}=1 + 27=28$;
当$m = 3$,$n = 1$时,$a=m^{2}+3n^{2}=3^{2}+3×1^{2}=9 + 3=12$。
【答案】:
(1)$m^{2}+3n^{2}$;$2mn$;
(2)$4$;$2$;
(3)$12$或$28$
(1)
已知$a + b\sqrt{3}=(m + n\sqrt{3})^2$,根据完全平方公式$(A + B)^2=A^{2}+2AB + B^{2}$,将$(m + n\sqrt{3})^2$展开可得:
$(m + n\sqrt{3})^2=m^{2}+2× m× n\sqrt{3}+(n\sqrt{3})^{2}=m^{2}+2mn\sqrt{3}+3n^{2}$。
因为$a + b\sqrt{3}=m^{2}+3n^{2}+2mn\sqrt{3}$,所以$a = m^{2}+3n^{2}$,$b = 2mn$。
(2)
当$a = 7$,$n = 1$时,由$a=m^{2}+3n^{2}$可得:
$7=m^{2}+3×1^{2}$,即$m^{2}+3 = 7$,移项可得$m^{2}=7 - 3=4$,因为$m$为正整数,所以$m = 2$。
由$b = 2mn$,把$m = 2$,$n = 1$代入可得$b=2×2×1 = 4$。
所以$7 + 4\sqrt{3}=(2+\sqrt{3})^2$。
(3)
因为$a + 6\sqrt{3}=(m + n\sqrt{3})^2=m^{2}+3n^{2}+2mn\sqrt{3}$,所以$b = 2mn=6$,则$mn = 3$。
因为$m$,$n$均为正整数,所以有两种情况:
当$m = 1$,$n = 3$时,$a=m^{2}+3n^{2}=1^{2}+3×3^{2}=1 + 27=28$;
当$m = 3$,$n = 1$时,$a=m^{2}+3n^{2}=3^{2}+3×1^{2}=9 + 3=12$。
【答案】:
(1)$m^{2}+3n^{2}$;$2mn$;
(2)$4$;$2$;
(3)$12$或$28$
查看更多完整答案,请扫码查看


