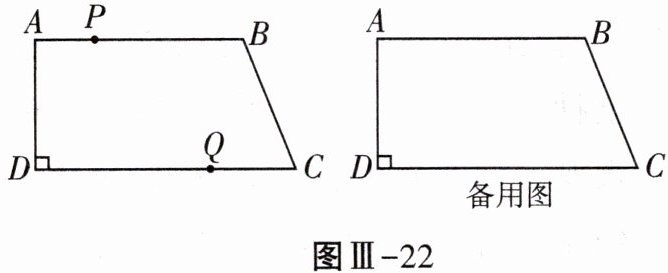
24. (10分)如图Ⅲ-22,在四边形ABCD中,$AB// CD,∠ADC= 90^{\circ },AD= 12cm,AB= 18cm,CD= 23cm$,动点P从点A出发,以1cm/s的速度向点B运动,同时动点Q从点C出发,以2cm/s的速度向点D运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为ts.
(1)当$t= 3$时,$PB= $____cm.
(2)当t为何值时,直线PQ把四边形ABCD分成两个部分,且其中的一部分是平行四边形?
(3)四边形PBQD能否成为菱形?若能,求出t的值;若不能,请说明理由.
(1)当$t= 3$时,$PB= $____cm.
(2)当t为何值时,直线PQ把四边形ABCD分成两个部分,且其中的一部分是平行四边形?
(3)四边形PBQD能否成为菱形?若能,求出t的值;若不能,请说明理由.

答案:
解:
(1) 当$ t = 3 $时,则$ AP = 3 × 1 = 3 \mathrm { cm } $,
$ \therefore PB = AB - AP = 18 - 3 = 15 \mathrm { cm } $,
故答案为:15。
(2) 若四边形$ PBCQ $是平行四边形,
$ \therefore PB = CQ $,$ \therefore 18 - t = 2 t $,$ \therefore t = 6 $,
若四边形$ PQDA $是平行四边形,
$ \therefore AP = DQ $,$ \therefore t = 23 - 2 t $,$ \therefore t = \frac { 23 } { 3 } $,
综上所述:$ t = 6 $或$ \frac { 23 } { 3 } $;
(3) 如图答图Ⅲ-2,
若四边形$ PBQD $是菱形,
$ \therefore BP = DP $,
$ \because AP ^ { 2 } + AD ^ { 2 } = DP ^ { 2 } $,
$ \therefore AP ^ { 2 } + 144 = ( 18 - AP ) ^ { 2 } $,
$ \therefore AP = 5 $,
$ \therefore t = \frac { 5 } { 1 } = 5 $,
$ \therefore $当$ t = 5 $时,四边形$ PBQD $为菱形。

解:
(1) 当$ t = 3 $时,则$ AP = 3 × 1 = 3 \mathrm { cm } $,
$ \therefore PB = AB - AP = 18 - 3 = 15 \mathrm { cm } $,
故答案为:15。
(2) 若四边形$ PBCQ $是平行四边形,
$ \therefore PB = CQ $,$ \therefore 18 - t = 2 t $,$ \therefore t = 6 $,
若四边形$ PQDA $是平行四边形,
$ \therefore AP = DQ $,$ \therefore t = 23 - 2 t $,$ \therefore t = \frac { 23 } { 3 } $,
综上所述:$ t = 6 $或$ \frac { 23 } { 3 } $;
(3) 如图答图Ⅲ-2,
若四边形$ PBQD $是菱形,
$ \therefore BP = DP $,
$ \because AP ^ { 2 } + AD ^ { 2 } = DP ^ { 2 } $,
$ \therefore AP ^ { 2 } + 144 = ( 18 - AP ) ^ { 2 } $,
$ \therefore AP = 5 $,
$ \therefore t = \frac { 5 } { 1 } = 5 $,
$ \therefore $当$ t = 5 $时,四边形$ PBQD $为菱形。

25. (10分)阅读:在平面直角坐标系中,以任意两点$P(x_{1},y_{1}),Q(x_{2},y_{2})为端点的线段中点坐标为(\frac {x_{1}+x_{2}}{2},\frac {y_{1}+y_{2}}{2})$.
运用:(1)如图Ⅲ-24,矩形ONEF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点E的坐标为$(4,3)$,则点M的坐标为____
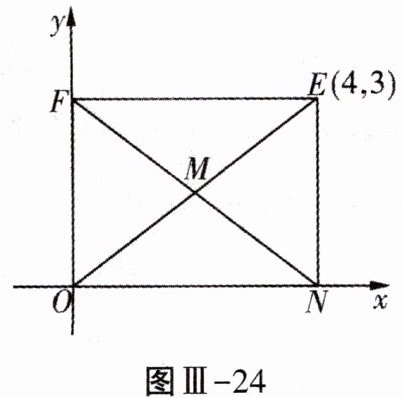
(2)在平面直角坐标系中,有$A(-1,2),B(3,1),C(1,4)$三点,另有一点D与点A,B,C构成平行四边形,求点D的坐标.
解:设点$ D $的坐标为$ ( x , y ) $,
当$ AB $为一条对角线时,$ AB $的中点坐标为$ \left( 1 , \frac { 3 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x + 1 } { 2 } = 1 , } \\ { \frac { y + 4 } { 2 } = \frac { 3 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 1 , } \\ { y = - 1 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 1 , - 1 ) $。
当$ AC $为一条对角线时,$ AC $的中点坐标为$ ( 0 , 3 ) $,则$ \left\{ \begin{array} { l } { \frac { x + 3 } { 2 } = 0 , } \\ { \frac { y + 1 } { 2 } = 3 , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = - 3 , } \\ { y = 5 , } \end{array} \right. $
此时点$ D $的坐标为$ ( - 3 , 5 ) $。
当$ BC $为一条对角线时,$ BC $的中点坐标为$ \left( 2 , \frac { 5 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x - 1 } { 2 } = 2 , } \\ { \frac { y + 2 } { 2 } = \frac { 5 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 5 , } \\ { y = 3 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 5 , 3 ) $。
综上所述,点$ D $的坐标为
运用:(1)如图Ⅲ-24,矩形ONEF的对角线相交于点M,ON,OF分别在x轴和y轴上,O为坐标原点,点E的坐标为$(4,3)$,则点M的坐标为____
$\left( 2 , \frac { 3 } { 2 } \right)$
.
(2)在平面直角坐标系中,有$A(-1,2),B(3,1),C(1,4)$三点,另有一点D与点A,B,C构成平行四边形,求点D的坐标.
解:设点$ D $的坐标为$ ( x , y ) $,
当$ AB $为一条对角线时,$ AB $的中点坐标为$ \left( 1 , \frac { 3 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x + 1 } { 2 } = 1 , } \\ { \frac { y + 4 } { 2 } = \frac { 3 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 1 , } \\ { y = - 1 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 1 , - 1 ) $。
当$ AC $为一条对角线时,$ AC $的中点坐标为$ ( 0 , 3 ) $,则$ \left\{ \begin{array} { l } { \frac { x + 3 } { 2 } = 0 , } \\ { \frac { y + 1 } { 2 } = 3 , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = - 3 , } \\ { y = 5 , } \end{array} \right. $
此时点$ D $的坐标为$ ( - 3 , 5 ) $。
当$ BC $为一条对角线时,$ BC $的中点坐标为$ \left( 2 , \frac { 5 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x - 1 } { 2 } = 2 , } \\ { \frac { y + 2 } { 2 } = \frac { 5 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 5 , } \\ { y = 3 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 5 , 3 ) $。
综上所述,点$ D $的坐标为
$ ( 1 , - 1 ) $或$ ( - 3 , 5 ) $或$ ( 5 , 3 ) $
。
答案:
解:
(1)$ \left( 2 , \frac { 3 } { 2 } \right) $
(2) 设点$ D $的坐标为$ ( x , y ) $,
当$ AB $为一条对角线时,$ AB $的中点坐标为$ \left( 1 , \frac { 3 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x + 1 } { 2 } = 1 , } \\ { \frac { y + 4 } { 2 } = \frac { 3 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 1 , } \\ { y = - 1 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 1 , - 1 ) $。
当$ AC $为一条对角线时,$ AC $的中点坐标为$ ( 0 , 3 ) $,则$ \left\{ \begin{array} { l } { \frac { x + 3 } { 2 } = 0 , } \\ { \frac { y + 1 } { 2 } = 3 , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = - 3 , } \\ { y = 5 , } \end{array} \right. $
此时点$ D $的坐标为$ ( - 3 , 5 ) $。
当$ BC $为一条对角线时,$ BC $的中点坐标为$ \left( 2 , \frac { 5 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x - 1 } { 2 } = 2 , } \\ { \frac { y + 2 } { 2 } = \frac { 5 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 5 , } \\ { y = 3 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 5 , 3 ) $。
综上所述,点$ D $的坐标为$ ( 1 , - 1 ) $或$ ( - 3 , 5 ) $或$ ( 5 , 3 ) $。
(1)$ \left( 2 , \frac { 3 } { 2 } \right) $
(2) 设点$ D $的坐标为$ ( x , y ) $,
当$ AB $为一条对角线时,$ AB $的中点坐标为$ \left( 1 , \frac { 3 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x + 1 } { 2 } = 1 , } \\ { \frac { y + 4 } { 2 } = \frac { 3 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 1 , } \\ { y = - 1 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 1 , - 1 ) $。
当$ AC $为一条对角线时,$ AC $的中点坐标为$ ( 0 , 3 ) $,则$ \left\{ \begin{array} { l } { \frac { x + 3 } { 2 } = 0 , } \\ { \frac { y + 1 } { 2 } = 3 , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = - 3 , } \\ { y = 5 , } \end{array} \right. $
此时点$ D $的坐标为$ ( - 3 , 5 ) $。
当$ BC $为一条对角线时,$ BC $的中点坐标为$ \left( 2 , \frac { 5 } { 2 } \right) $,则$ \left\{ \begin{array} { l } { \frac { x - 1 } { 2 } = 2 , } \\ { \frac { y + 2 } { 2 } = \frac { 5 } { 2 } , } \end{array} \right. $解得$ \left\{ \begin{array} { l } { x = 5 , } \\ { y = 3 , } \end{array} \right. $
此时点$ D $的坐标为$ ( 5 , 3 ) $。
综上所述,点$ D $的坐标为$ ( 1 , - 1 ) $或$ ( - 3 , 5 ) $或$ ( 5 , 3 ) $。
查看更多完整答案,请扫码查看


