搜索
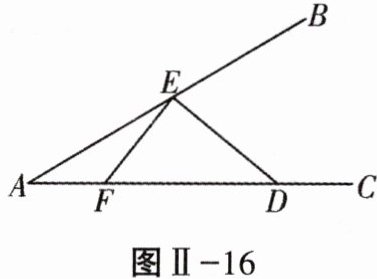
23. (10分)如图Ⅱ-16,$∠BAC= 30^{\circ }$,E为射线AB上一个动点,F为射线AC上一个动点,$AD= 6$,求$DE+EF$的最小值.
答案：
解：如答图Ⅱ - 6，作 $AD$ 关于 $AB$ 的对称线 $AD'$，作 $D'F \perp AC$，垂足为 $F$，交 $AB$ 于点 $E$，则 $D'F$ 为 $EF + DE$ 的最小值。
$\because AD = AD' = 6$，$\angle D'AD = 60^{\circ}$，$AF = 3$，$\therefore$ 在 $Rt\triangle AD'F$ 中，$D'F = \sqrt{D'A^2 - AF^2} = 3\sqrt{3}$。故 $DE + EF$ 的最小值为 $3\sqrt{3}$。
解：如答图Ⅱ - 6，作 $AD$ 关于 $AB$ 的对称线 $AD'$，作 $D'F \perp AC$，垂足为 $F$，交 $AB$ 于点 $E$，则 $D'F$ 为 $EF + DE$ 的最小值。
$\because AD = AD' = 6$，$\angle D'AD = 60^{\circ}$，$AF = 3$，$\therefore$ 在 $Rt\triangle AD'F$ 中，$D'F = \sqrt{D'A^2 - AF^2} = 3\sqrt{3}$。故 $DE + EF$ 的最小值为 $3\sqrt{3}$。 24. (10分)如图Ⅱ-17,图(1)是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边$BC= 5$,将四个直角三角形中较长的直角边分别向外延长一倍,得到图(2)所示的“数学风车”,若$△BCD$的周长是30,则这个风车的外围周长是
76
.
答案：
解：设 $AC = AD = x$，则 $BD = 30 - 5 - 2x = 25 - 2x$，$\because BD^2 = BC^2 + CD^2$，$\therefore 5^2 + (2x)^2 = (25 - 2x)^2$，$\therefore x = 6$，$\therefore BD = 25 - 2x = 13$，$AD = 6$，$\therefore$ 这个风车的外围周长是：$(13 + 6) × 4 = 76$。
25. (10分)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)下列四边形是勾股四边形的有____.(填序号)
①长方形;②平行四边形;③正方形;
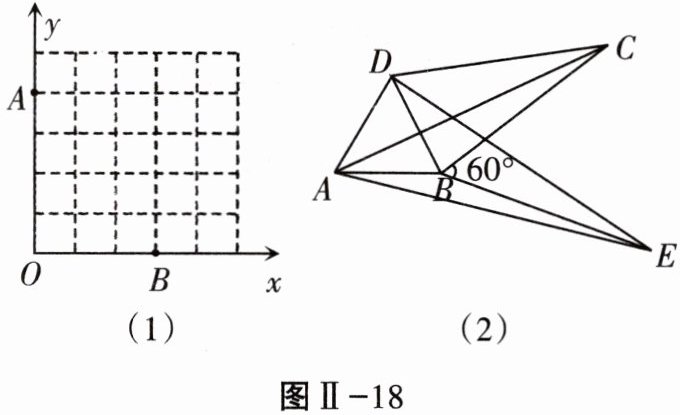
(2)如图Ⅱ-18(1),已知格点(小正方形的顶点)$O(0,0),A(0,4),B(3,0)$,请你直接写出所有以格点为顶点,OA,OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标____.
(3)如图Ⅱ-18(2),将$△ABC$绕顶点B按顺时针方向旋转$60^{\circ }$,得到$△DBE$,连接AD,DC,已知$∠DCB= 30^{\circ }$.求证:四边形ABCD是勾股四边形.
(1)下列四边形是勾股四边形的有____.(填序号)
①长方形;②平行四边形;③正方形;
(2)如图Ⅱ-18(1),已知格点(小正方形的顶点)$O(0,0),A(0,4),B(3,0)$,请你直接写出所有以格点为顶点,OA,OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标____.
(3)如图Ⅱ-18(2),将$△ABC$绕顶点B按顺时针方向旋转$60^{\circ }$,得到$△DBE$,连接AD,DC,已知$∠DCB= 30^{\circ }$.求证:四边形ABCD是勾股四边形.
答案：
①③；
(2) 如答图Ⅱ - 7 所示：$M(3, 4)$ 或 $(4, 3)$；
(3) 证明：如答图Ⅱ - 8，连接 $CE$，由旋转得：$\triangle ABC \cong \triangle DBE$，$\therefore AC = DE$，$BC = BE$，$\because \angle CBE = 60^{\circ}$，$\therefore \triangle CBE$ 为等边三角形，$\therefore BC = CE$，$\angle BCE = 60^{\circ}$，$\because \angle DCB = 30^{\circ}$，$\therefore \angle DCE = \angle DCB + \angle BCE = 30^{\circ} + 60^{\circ} = 90^{\circ}$，$\therefore DC^2 + EC^2 = DE^2$，$\therefore DC^2 + BC^2 = AC^2$，即四边形 $ABCD$ 是勾股四边形。
①③；
(2) 如答图Ⅱ - 7 所示：$M(3, 4)$ 或 $(4, 3)$；
(3) 证明：如答图Ⅱ - 8，连接 $CE$，由旋转得：$\triangle ABC \cong \triangle DBE$，$\therefore AC = DE$，$BC = BE$，$\because \angle CBE = 60^{\circ}$，$\therefore \triangle CBE$ 为等边三角形，$\therefore BC = CE$，$\angle BCE = 60^{\circ}$，$\because \angle DCB = 30^{\circ}$，$\therefore \angle DCE = \angle DCB + \angle BCE = 30^{\circ} + 60^{\circ} = 90^{\circ}$，$\therefore DC^2 + EC^2 = DE^2$，$\therefore DC^2 + BC^2 = AC^2$，即四边形 $ABCD$ 是勾股四边形。
查看更多完整答案，请扫码查看
