7. 如图4-5,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是
$\frac{24}{5}$
.
答案:
$\frac{24}{5}$
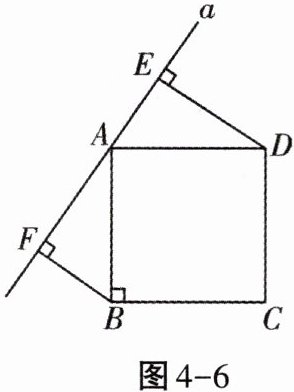
8. 如图4-6,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B,D作BF⊥a,垂足为F,DE⊥a,垂足为E.若DE= 8,BF= 5,则EF的长为______
13
.
答案:
13
9. 如图4-7,在矩形ABCD中,点E,F分别在边CD,BC上,且DC= 3DE= 9,将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP的长为______
$6\sqrt{3}$
.
答案:
$6\sqrt{3}$
10. 如图4-8,在边长为4的正方形ABCD中,点P是对角线BD上一动点,点E在边CD上,EC= 1,则PC+PE的最小值是
5
.
答案:
5
11. 如图4-9,在正方形ABCD中,M,N分别是边AD,CD的中点,连接BM,AN交于点E.求证:AN⊥BM.
证明:∵∠BAD=∠D=90°, BA=AD=DC,
又∵点M,N分别是AD,CD的中点,
∴AM=DN=1/2AD,∴△ABM≌△DAN,
∴∠ABM=∠DAN;∵∠BAN+∠DAN=90°,
∴∠BAN+∠ABM=90°,∴∠AEB=90°,即AN⊥BM.
证明:∵∠BAD=∠D=90°, BA=AD=DC,
又∵点M,N分别是AD,CD的中点,
∴AM=DN=1/2AD,∴△ABM≌△DAN,
∴∠ABM=∠DAN;∵∠BAN+∠DAN=90°,
∴∠BAN+∠ABM=90°,∴∠AEB=90°,即AN⊥BM.
答案:
证明:$\because \angle BAD=\angle D=90^{\circ}, BA=AD=DC$,
又$\because$点$M$,$N$分别是$AD$,$CD$的中点,
$\therefore AM=DN=\frac{1}{2}AD$,$\therefore \triangle ABM\cong \triangle DAN$,
$\therefore \angle ABM=\angle DAN$;$\because \angle BAN+\angle DAN=90^{\circ}$,
$\therefore \angle BAN+\angle ABM=90^{\circ}$,$\therefore \angle AEB=90^{\circ}$,即$AN\perp BM$.
又$\because$点$M$,$N$分别是$AD$,$CD$的中点,
$\therefore AM=DN=\frac{1}{2}AD$,$\therefore \triangle ABM\cong \triangle DAN$,
$\therefore \angle ABM=\angle DAN$;$\because \angle BAN+\angle DAN=90^{\circ}$,
$\therefore \angle BAN+\angle ABM=90^{\circ}$,$\therefore \angle AEB=90^{\circ}$,即$AN\perp BM$.
12. 如图4-10,已知□ABCD的对角线AC,BD相交于点O,∠OBC= ∠OCB.
(1)求证:□ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
(1)求证:□ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
AC⊥BD或AB=BC
答案:
(1)证明:$\because \angle OBC=\angle OCB$,
$\therefore BO=CO$.又$\because$在$□ ABCD$中,
$\therefore AO=CO$,$DO=BO$,$\therefore 2BO=2AO$,
即$BD=AC$,$\therefore □ ABCD$为矩形.
(2)解:$AC\perp BD$或$AB=BC$.
(1)证明:$\because \angle OBC=\angle OCB$,
$\therefore BO=CO$.又$\because$在$□ ABCD$中,
$\therefore AO=CO$,$DO=BO$,$\therefore 2BO=2AO$,
即$BD=AC$,$\therefore □ ABCD$为矩形.
(2)解:$AC\perp BD$或$AB=BC$.
查看更多完整答案,请扫码查看


