《2025年暑假作业兰州大学出版社八年级数学人教版》

3. 若一次函数$y = ax + b的图象与一次函数y = mx + n$的图象相交,且交点在$x$轴上,则$a$,$b$,$m$,$n$满足的关系式是$an = bm$.

答案： $an = bm$ 解析:设交点为$(x,0)$，$ax + b = 0$①，$mx + n = 0$②，①$×m -$②$×a$得：$mb - an = 0$，$an = bm$.

4. 如果$M(x_1,y_1)$,$N(x_2,y_2)是一次函数y = 3x - 8$图象上的两点,且$x_1 + x_2 = - 3$,那么$y_1 + y_2 = $$-25$.

答案： $-25$ 解析:根据题意得$y_{1} + y_{2} = 3(x_{1} + x_{2}) - 16 = 3×(-3) - 16 = -25$.

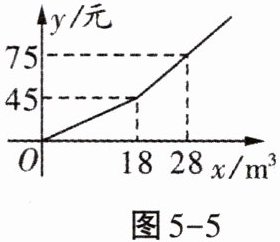
5. 某市规定了每月用水$18\mathrm{m}^3$以内(含$18\mathrm{m}^3$)和用水$18\mathrm{m}^3$以上两种不同的收费标准. 该市的用户每月应交水费$y$(元)是用水量$x(\mathrm{m}^3)$的函数,其图象如图5 - 5所示.

(1)若某月用水量为$18\mathrm{m}^3$,则应交水费45元？
(2)求当$x ＞ 18$时,$y关于x$的函数解析式. 若小敏家某月交水费$81$元,则这个月的用水量为30立方米？

答案： 解:
(1)观察函数图象可得当横坐标为18时，纵坐标为45，即应交水费为45元.
(2)设当$x ＞ 18$时，$y$关于$x$的函数解析式为$y = kx + b(k≠0)$，
将$(18,45)$和$(28,75)$代入可得$\left\{\begin{array}{l} 18k + b = 45\\ 28k + b = 75\end{array}\right.$，
解得$\left\{\begin{array}{l} k = 3\\ b = -9\end{array}\right.$，
则当$x ＞ 18$时，$y$关于$x$的函数解析式为$y = 3x - 9$，
当$y = 81$时，$3x - 9 = 81$，解得$x = 30$.
答:这个月的用水量为$30m^{3}$.

(1)已知$f(x) = - 2x^2 - 3x + 1$,求$f( - 2)$值；-1
(2)已知$f(x) = ax^3 + 2x^2 - ax - 6$,当$f(\frac{1}{2}) = a$,求$a$的值；-4
(3)已知$f(x) = \frac{2kx + a}{3} - \frac{x - bk}{6} - 2$($a$、$b$为常数),若对于任意有理数$k$,总有$f(1) = 0$,求$a$、$b$的值.$a=6.5$，$b=-4$

答案：
(1)解:
(1)把$x = -2$代入得，
$f(-2)= -8 + 6 + 1 = -1$ $\therefore f(-2)= -1$;
(2)把$x = \frac{1}{2}$，$f(\frac{1}{2}) = a$代入得，
$f(\frac{1}{2}) = (\frac{1}{2})^{3}a + 2×(\frac{1}{2})^{2} - \frac{1}{2}a - 6 = a$
即$\frac{1}{8}a + \frac{1}{2} - \frac{1}{2}a - 6 = a$ 解得:$a = -4$;
(3)把$x = 1$，$f(1) = 0$代入得，
$f(1)=\frac{2k + a}{3}-\frac{1 - bk}{6}-2 = 0$，整理得
$(4 + b)k + 2a = 13$
$\because a$、$b$为常数，对于任意有理数$k$，总有$f(1) = 0$
$\therefore 4 + b = 0$ $\therefore b = -4$ $\therefore a = 6.5$.