《2025年暑假作业兰州大学出版社八年级数学人教版》

1. 若一组数据1,a,2,3,4的平均数与中位数相同,则a不可能是下列选项中的(C)
A.0
B.2.5
C.3
D.5

答案： C

2. 李华根据演讲比赛中九位评委所给的分数制作了如下表格：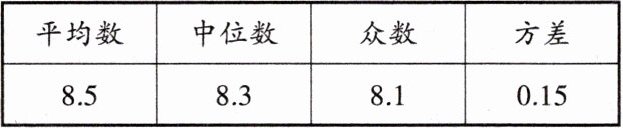
若要去掉一个最高分和一个最低分,则表中数据一定不发生变化的是(D)
A.平均数
B.众数
C.方差
D.中位数

答案： D

3. 已知一组数据$x_{1}$,$x_{2}$,$x_{3}$,$x_{4}$的平均数是5,则数据$x_{1}+3$,$x_{2}+3$,$x_{3}+3$,$x_{4}+3$的平均数是8.

答案： 8

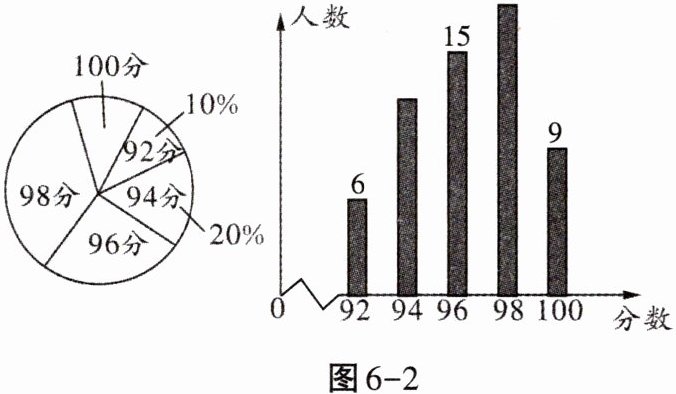
4. 某单位若干名职工参加普法知识竞赛,将成绩制成如图6-2所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数是96分,平均数是96.4分.

答案： 96分,96.4分

5. 甲、乙两名队员参加射击训练,成绩分别被制成图6-3所示的两个统计图：

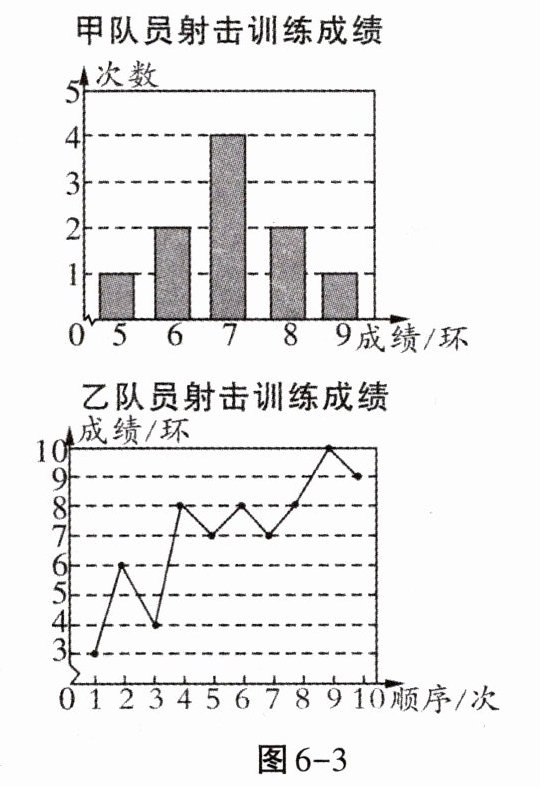
根据以上信息,整理分析数据如下：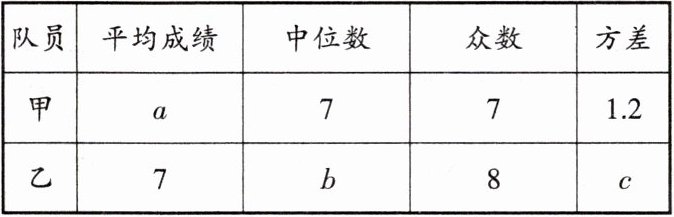
(1)写出表格中a,b,c的值；a=7，b=7.5，c=4.2；
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩. 若选派其中一名参赛,你认为应选哪名队员？从平均成绩看，甲、乙二人的成绩相等，均为7环；从中位数看，甲射中7环以上的次数小于乙；从众数看，甲射中7环的次数最多；而乙射中8环的次数最多；从方差看甲的成绩比乙的成绩稳定.综合以上各因素，若选派一名队员参加比赛，可选择乙参赛，因为乙获得高分的可能更大.

答案： 解:
(1)甲的平均成绩为$a=\frac {5×1 + 6×2 + 7×4 + 8×2 + 9×1}{1 + 2 + 4 + 2 + 1}=7$(环)，
∵乙射击的成绩从小到大排列为：3，4，6，7，7，8，8，8，9，10，
∴乙射击成绩的中位数$b=\frac {7 + 8}{2}=7.5$(环)，
乙射击成绩的方差为
$c=\frac {1}{10}×[(3 - 7)^{2}+(4 - 7)^{2}+(6 - 7)^{2}+2×(7 - 7)^{2}+3×(8 - 7)^{2}+(9 - 7)^{2}+(10 - 7)^{2}]=\frac {1}{10}×(16 + 9 + 1 + 3 + 4 + 9)=4.2$.
(2)从平均成绩看，甲、乙二人的成绩相等，均为7环；从中位数看，甲射中7环以上的次数小于乙；从众数看，甲射中7环的次数最多；而乙射中8环的次数最多；从方差看甲的成绩比乙的成绩稳定.综合以上各因素，若选派一名队员参加比赛，可选择乙参赛，因为乙获得高分的可能更大.