《2025年暑假作业兰州大学出版社八年级数学人教版》

13. 如图4-11,在矩形ABCD中,E,F分别是AD,BC的中点,CE,AF分别交BD于G,H两点.
求证：(1)四边形AFCE是平行四边形；
(2)EG= FH.
证明:(1)∵四边形ABCD是矩形，
∴AD// BC,AD=BC.
∵E,F分别是AD,BC的中点,
∴AE=1/2AD,CF=1/2BC,∴AE=CF,
∴四边形AFCE是平行四边形.
(2)∵四边形AFCE是平行四边形，
∴CE// AF,∴∠DGE=∠AHD=∠BHF.
∵AD// BC,∴∠EDG=∠FBH.
在△DEG和△BFH中,{∠DGE=∠BHF,∠EDG=∠FBH,DE=BF,
∴△DEG≌△BFH(AAS),∴EG=FH.

答案： 证明:
(1)$\because$四边形$ABCD$是矩形，
　　$\therefore AD// BC$,$AD=BC$.
　　$\because E$,$F$分别是$AD$,$BC$的中点,
　　$\therefore AE=\frac{1}{2}AD$,$CF=\frac{1}{2}BC$,$\therefore AE=CF$,
　　$\therefore$四边形$AFCE$是平行四边形.
(2)$\because$四边形$AFCE$是平行四边形，
　　$\therefore CE// AF$,$\therefore \angle DGE=\angle AHD=\angle BHF$.
　　$\because AD// BC$,$\therefore \angle EDG=\angle FBH$.
　　在$\triangle DEG$和$\triangle BFH$中,$\left\{\begin{array}{l}\angle DGE=\angle BHF,\\ \angle EDG=\angle FBH,\\ DE=BF,\end{array}\right.$
　　$\therefore \triangle DEG\cong \triangle BFH(AAS)$,$\therefore EG=FH$.

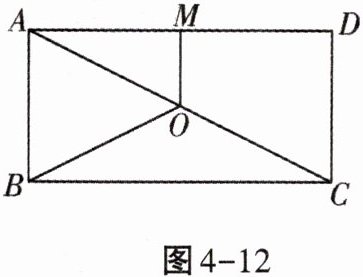
1. 如图4-12,点O是矩形ABCD的对角线AC的中点,OM//AB交AD于点M,若OM= 3,BC= 10,则OB的长为(D)

A.5
B.4
C.√34/2
D.√34

答案： D

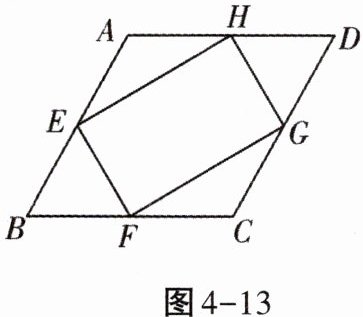
2. 如图4-13,在菱形ABCD中,∠ABC= 60°,AB= 4.若点E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE,则四边形EFGH的面积为(C)

A.8
B.6√3
C.4√3
D.6

答案： C

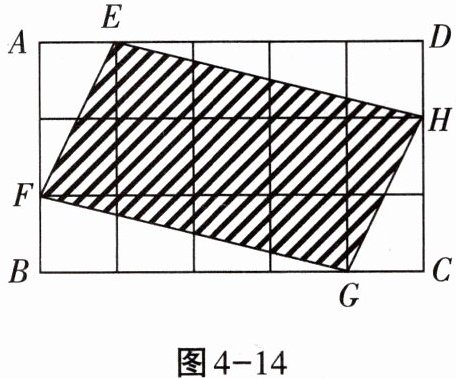
3. 如图4-14,将矩形ABCD分成15个大小相等的正方形,E,F,G,H分别在AD,AB,BC,CD边上,且都是某个小正方形的顶点,若四边形EFGH的面积为1,则矩形ABCD的面积为(C)

A.2
B.3
C.5/3
D.7/3

答案： C