《2025年暑假作业兰州大学出版社八年级数学人教版》

18. (12分)如图3-29,在$□ ABCD$中,$BD\perp AD$,$\angle A= 45^{\circ}$,$E$,$F分别是AB$,$CD$上的点,且$BE= DF$,连接$EF$,交$BD于O$。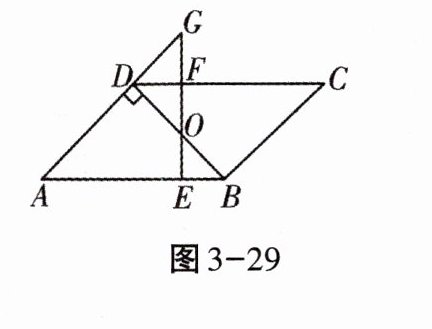
(1)求证：$BO= DO$；
(2)若$EF\perp AB$,延长$EF交AD的延长线于点G$,当$FG= 1$时,求$AD$的长。$2\sqrt{2}$

答案：
(1)证明:
∵四边形ABCD是平行四边形,
∴DC=AB,DC//AB,
∴∠ODF=∠OBE.
在△ODF与△OBE中,
$\left\{\begin{array}{l} ∠ODF=∠OBE,\\ ∠DOF=∠BOE,\\ DF=BE,\end{array}\right.$
∴△ODF≌△OBE(AAS),
∴BO=DO.
(2)解:
∵BD⊥AD,
∴∠ADB=90°.
∵∠A=45°,
∴∠DBA=∠A=45°.
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形.
∵AB//CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∴DF=FG=1,
∴DG=$\sqrt{DF^{2}+FG^{2}}=\sqrt{2}$.
∵DG=DO=$\sqrt{2}$,又
∵DO=BO,
∴AD=2DO=2$\sqrt{2}$.

19. (12分)问题探究
(1)如图3-30①,在$□ ABCD外分别作等腰直角三角形ABF和等腰直角三角形ADE$,$\angle FAB= \angle EAD= 90^{\circ}$,连接$AC$,$EF$。在图中找一个与$\triangle FAE$全等的三角形,并加以证明。
问题解决
(2)以$□ ABCD$的四条边为边,向外分别作正方形,如图3-30②,连接$EF$,$GH$,$IJ$,$KL$。若$□ ABCD$的面积为5,则图中阴影部分四个三角形的面积和为______10。

答案： 解:
(1)△ABC(或△CDA)与△FAE全等
(下面仅对△ABC≌△FAE证明)
∵∠FAB=∠EAD=90°,
∴∠EAF+∠DAB=180°.
∵四边形ABCD是平行四边形，
∴AD//BC,AD=BC,
∴∠DAB+∠CBA=180°,
∴∠CBA=∠EAF.
∵AE=AD,
∴BC=AE.
又
∵AB=AF,
∴△ABC≌△FAE.
(2)由
(1)同理可得,△AEF≌△DAC≌△CIJ,△BGH≌△DKL≌△CDB,则四个三角形面积和为$\frac{1}{2}$×5×4=10.