《2025年暑假作业兰州大学出版社八年级数学人教版》

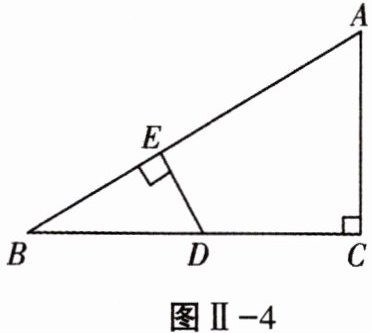
7. 如图Ⅱ-4,在$△ABC$中,$∠C= 90^{\circ }$,D为BC边的中点,$DE⊥AB$,垂足为E,则$AE^{2}-BE^{2}$等于 (B)

A.$BD^{2}$
B.$AC^{2}$
C.$BC^{2}$
D.$DE^{2}$

答案： B 解析：连接 $AD$，在 $Rt\triangle AED$ 中有：$AE^2 = AD^2 - DE^2$，在 $Rt\triangle EBD$ 中有：$BE^2 = BD^2 - DE^2$，又 $BD = CD$，$\therefore AE^2 - BE^2 = AD^2 - DE^2 - BD^2 + DE^2 = AD^2 - BD^2$ $= AD^2 - CD^2 = AC^2$。

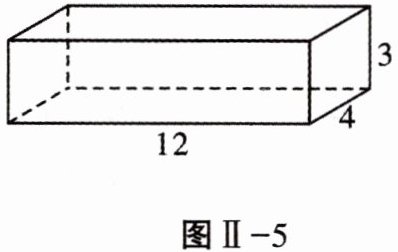
8. 如图Ⅱ-5,一个长方体木箱的长、宽、高分别为12m,4m,3m,则能放进此木箱中的木棒最长为 (A)

A.13m
B.15m
C.19m
D.24m

答案： A 解析：$3^2 + 4^2 + 12^2 = 169 = 13^2$。

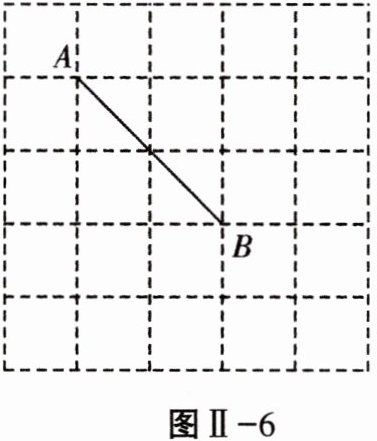
9. 如图Ⅱ-6,在$5×5$的正方形网格中,以AB为边画$Rt△ABC$,使点C在格点上,满足这样条件的点C的个数是 (C)

A.6
B.7
C.8
D.9

答案： C 解析：分三类，当点 $A$ 处是直角时，有 $2$ 个点；当点 $B$ 处是直角时，有 $4$ 个点；当点 $C$ 处是直角时，有 $2$ 个点，故共有 $2 + 4 + 2 = 8$ 个点。

10. 已知$Rt△ABC$中,a,b为直角边,c为斜边,h为斜边上的高,则下面说法错误的是 (B)
A.以ah,bh,ab为边的三角形是直角三角形
B.以$a+b,ab,c$为边的三角形是直角三角形
C.以$\frac {1}{a},\frac {1}{b},\frac {1}{h}$为边的三角形是直角三角形
D.以$c+h,a+b,h$为边的三角形是直角三角形

答案： B

11. 如果梯子的底端离建筑物9m,那么15m长的梯子可以到达建筑物的高度是12m.

答案： 12m

12. 已知$△ABC$中,$a:b:c= 15:8:17$,若$△ABC$的面积为240,则此三角形的周长是80.

答案： 80 解析：由 $a : b : c = 15 : 8 : 17$ 可知 $\triangle ABC$ 是直角三角形，$\therefore$ 设两条直角边为 $8x$ 和 $15x$。$\because \triangle ABC$ 的面积为 $240$，$\therefore \frac{1}{2} × 8x × 15x = 240$，解得 $x = 2$，$\therefore \triangle ABC$ 的三边长为 $16$，$30$，$34$，$\therefore \triangle ABC$ 的周长为 $80$。