《2025年暑假作业兰州大学出版社八年级数学人教版》

1. 如果一次函数$y = kx + b$($k$,$b$是常数,$k \neq 0$)的图象经过第一、二、四象限,那么$k$,$b$应满足的条件是(B)
A.$k ＞ 0且b ＞ 0$
B.$k ＜ 0且b ＞ 0$
C.$k ＞ 0且b ＜ 0$
D.$k ＜ 0且b ＜ 0$

答案： B

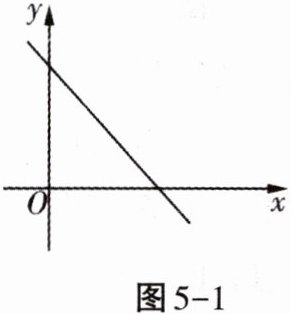
2. 一次函数$y = (m - 2)x + 3$的图象如图5 - 1所示,则$m$的取值范围是(A)

A.$m ＜ 2$
B.$0 ＜ m ＜ 2$
C.$m ＜ 0$
D.$m ＞ 2$

答案： A 解析:一次函数$y=(m - 2)x + 3$的图象经过第一、二、四象限，$\therefore m - 2 ＜ 0$，解得$m ＜ 2$.

3. 将一次函数$y = 2x - 3的图象沿y$轴向上平移8个单位长度,所得直线的解析式为(B)
A.$y = 2x - 5$
B.$y = 2x + 5$
C.$y = 2x + 8$
D.$y = 2x - 8$

答案： B 解析:根据函数图象上加下减的平移法则，可得$y = 2x - 3 + 8$，即$y = 2x + 5$.

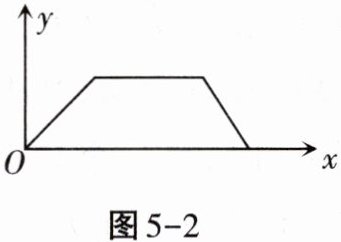
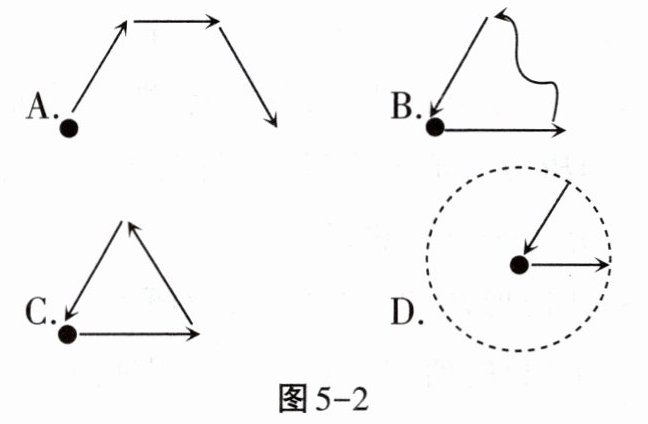
4. 图5 - 2是张老师出门散步时离家的距离$y与时间x$之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是(D)

答案： D

5. 目前,全球淡水资源日益减少,提倡全社会节约用水. 据测试：拧不紧的水龙头每分钟滴出100滴水,每滴水约$0.05\mathrm{mL}$. 小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开$x\mathrm{min}$后,水龙头滴出$y\mathrm{mL}$的水,则$y与x$之间的函数关系式是(B)
A.$y = 0.05x$
B.$y = 5x$
C.$y = 100x$
D.$y = 0.05x + 100$

答案： B

6. 我们规定：当$k$,$b$为常数,$k \neq 0$,$b \neq 0$,$k \neq b$时,一次函数$y = kx + b与y = bx + k$互为交换函数. 例如：$y = 4x + 3的交换函数为y = 3x + 4$. 一次函数$y = kx + 2$与它的交换函数图象的交点横坐标为______1.

答案： 1 解析:由题意可得$\left\{\begin{array}{l} y = kx + 2\\ y = 2x + k\end{array}\right.$，
解得$\left\{\begin{array}{l} x = 1\\ y = k + 2\end{array}\right.$，故答案为1.