《2025年暑假作业兰州大学出版社八年级数学人教版》

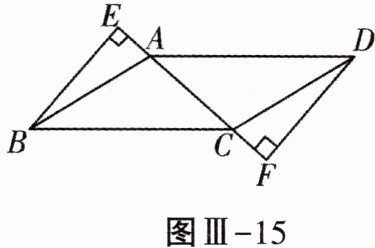
17. (6分)如图Ⅲ-15,在$□ ABCD$中,$BE⊥AC$,垂足为E,点E在CA的延长线上,$DF⊥AC$,垂足为F,点F在AC的延长线上,求证:$AE= CF$.

证明：∵四边形$ ABCD $是平行四边形，
$ \therefore AB // CD $，$ AB = CD $，$ \therefore \angle BAC = \angle DCA $，
$ \therefore 180^{\circ} - \angle BAC = 180^{\circ} - \angle DCA $，
$ \therefore \angle EAB = \angle DCF $，∵$ BE \perp AC $，$ DF \perp AC $，
$ \therefore \angle BEA = \angle DFC = 90^{\circ} $。
在$ \triangle BEA $和$ \triangle DFC $中，$ \left\{ \begin{array} { l } { \angle BEA = \angle DFC, } \\ { \angle EAB = \angle DCF, } \\ { AB = CD, } \end{array} \right. $
$ \therefore \triangle BEA \cong \triangle DFC ( $AAS$ ) $，$ \therefore AE = CF $。

答案： 证明：
∵四边形$ ABCD $是平行四边形，
$ \therefore AB // CD $，$ AB = CD $，$ \therefore \angle BAC = \angle DCA $，
$ \therefore 180^{\circ} - \angle BAC = 180^{\circ} - \angle DCA $，
$ \therefore \angle EAB = \angle DCF $，
∵$ BE \perp AC $，$ DF \perp AC $，
$ \therefore \angle BEA = \angle DFC = 90^{\circ} $。
在$ \triangle BEA $和$ \triangle DFC $中，$ \left\{ \begin{array} { l } { \angle BEA = \angle DFC, } \\ { \angle EAB = \angle DCF, } \\ { AB = CD, } \end{array} \right. $
$ \therefore \triangle BEA \cong \triangle DFC ( AAS ) $，$ \therefore AE = CF $。

18. (6分)如图Ⅲ-16,在$□ ABCD$中,点O是对角线AC、BD的交点,点E是CD的中点,点F在BC的延长线上,且$CF= \frac {1}{2}BC$,求证:四边形OCFE是平行四边形.
证明：∵四边形$ ABCD $是平行四边形，
$ \therefore $点$ O $是$ BD $的中点，又∵点$ E $是$ CD $的中点，
$ \therefore $OE是$ \triangle BCD $的中位线，
$ \therefore $OE // BC，且OE = \frac { 1 } { 2 } BC。
又$ \because CF = \frac { 1 } { 2 } BC $，$ \therefore $OE = CF。
又∵点$ F $在$ BC $的延长线上，$ \therefore $OE // CF，
$ \therefore $四边形$ OCFE $是平行四边形。

答案： 证明：
∵四边形$ ABCD $是平行四边形，
$ \therefore $点$ O $是$ BD $的中点，又
∵点$ E $是$ CD $的中点，
$ \therefore OE $是$ \triangle BCD $的中位线，
$ \therefore OE // BC $，且$ OE = \frac { 1 } { 2 } BC $。
又$ \because CF = \frac { 1 } { 2 } BC $，$ \therefore OE = CF $。
又
∵点$ F $在$ BC $的延长线上，$ \therefore OE // CF $，
$ \therefore $四边形$ OCFE $是平行四边形。

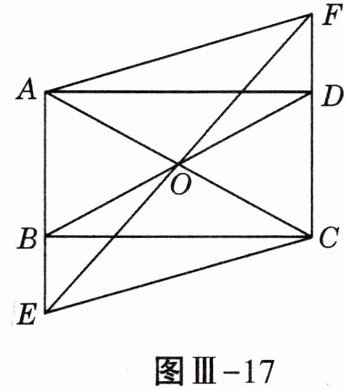
19. (8分)如图Ⅲ-17,在矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于点E,F.
求证:四边形AECF为平行四边形.

答案：
证明：如答图Ⅲ-1，连接$ AF $，$ EC $。

∵四边形$ ABCD $是矩形，$ \therefore OB = OD $。
又$ \because AE // CF $，$ \therefore \angle BEO = \angle DFO $，$ \angle OBE = \angle ODF $。
$ \therefore \triangle BOE \cong \triangle DOF ( AAS ) $，$ \therefore BE = DF $。
$ \because AB + BE = DC + DF $，$ \therefore AE = CF $，$ AE // CF $，
$ \therefore $四边形$ AECF $为平行四边形。

20. (8分)图Ⅲ-18①是某公交汽车挡风玻璃的雨刮器,其工作原理如图Ⅲ-18②.雨刷$EF⊥AD$,垂足为A,$AB= CD且AD= BC$,这样能使雨刷EF在运动时,始终垂直于玻璃窗下沿BC,请证明这一结论.
证明：$ \because AB = CD $，$ AD = BC $，$ \therefore $四边形$ ABCD $是平行四边形，$ \therefore AD // BC $，又$ \because EF \perp AD $，$ \therefore EF \perp BC $。

答案： 证明：$ \because AB = CD $，$ AD = BC $，
$ \therefore $四边形$ ABCD $是平行四边形，
$ \therefore AD // BC $，又$ \because EF \perp AD $，$ \therefore EF \perp BC $。