《2025年暑假作业兰州大学出版社八年级数学人教版》

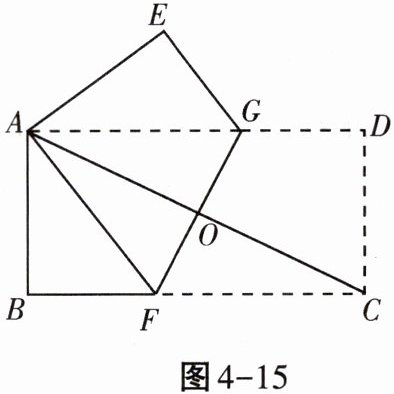
4. 如图4-15,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB= 4,BC= 8,则△ABF的面积为______6.

答案： 6

5. 已知正方形ABCD的边长为4,E是CD上一个动点,以点E为直角顶点,在正方形外侧等腰直角三角形CEF,连接BF,BD,FD.
(1)BD与CF的位置关系是平行.
(2)①如图4-16(1),当CE= 4(即点E与点D重合)时,△BDF的面积为8.
②如图4-16(2),当CE= 2(即点E为CD的中点)时,△BDF的面积为8.
③如图4-16(3),当CE= 3时,△BDF的面积为8.
(3)如图4-16(4),根据上述计算的结果,当E是CD上任意一点时,请提出你对△BDF面积与正方形ABCD的面积之间关系的猜想,并证明你的猜想.

答案： 解:
(1)正方形$ABCD$,等腰直角三角形$CEF$,
　　　$\therefore \angle ADC=\angle FDC=90^{\circ}$,
　　　$\therefore \angle ADC+\angle FDC=180^{\circ}$,
　　　即$A$、$D$、$F$三点共线,
　　　$\because DF// CB$,$DF=CD=BC$,
　　　$\therefore$四边形$BCFD$是平行四边形，
　　　$\therefore FC// BD$,
　　　故答案为:平行.
(2)①$\triangle BDF$的面积是$\frac{1}{2}DF× AB=\frac{1}{2}× 4× 4=8$,故答案为:8.
　　　②$\triangle BDF$的面积是:$S_{四边形BCFD}-S_{\triangle BCF}$
　　　$=S_{\triangle BDC}+S_{\triangle CDF}-S_{\triangle BCF}$
　　　$=\frac{1}{2}BC× DC+\frac{1}{2}CD× EF-\frac{1}{2}BC× CE$
　　　$=\frac{1}{2}× 4× 4+\frac{1}{2}× 4× 2-\frac{1}{2}× 4× 2=8$,
　　　故答案为:8.
　　　③与②求法类似:$\triangle BDF$的面积是$S_{\triangle BDC}+S_{\triangle CDF}-S_{\triangle BCF}$
　　　$=\frac{1}{2}BC× CD+\frac{1}{2}CD× EF-\frac{1}{2}CB× EF$
　　　$=\frac{1}{2}× 4× 4+\frac{1}{2}× 4× 3-\frac{1}{2}× 4× 3=8$,
　　　故答案为:8.
(3)$\triangle BDF$面积与正方形$ABCD$的面积之间关系是$S_{\triangle BDF}=\frac{1}{2}S_{正方形ABCD}$.
　　　证明:$\because S_{\triangle BDF}=8$,
　　　$S_{正方形ABCD}=BC× CD=4× 4=16$,
$\therefore S_{\triangle BDF}=\frac{1}{2}S_{正方形ABCD}$.