11. 计算:$3÷\sqrt{3}×\frac{1}{\sqrt{3}}=$
1
.
答案:
1
12. 比较大小:$-3\sqrt{2}$
<
$-2\sqrt{3}$(填“>”“<”或“=”).
答案:
<
13. 能使等式$\sqrt{\frac{x}{x - 2}}= \frac{\sqrt{x}}{\sqrt{x - 2}}成立的x$的取值范围是
$ x > 2 $
.
答案:
$ x > 2 $
14. 已知实数$x,y满足|x-4|+\sqrt{y - 8}= 0$,则以$x,y$的值为两边长的等腰三角形的周长是______
20
.
答案:
20
15. 已知$y= \sqrt{2x - 5}+\sqrt{5 - 2x}$,则$xy$的值为
0
.
答案:
0
16. 一个三角形的三边长分别为$\sqrt{8}$,$\sqrt{12}$,$\sqrt{18}$,则它的周长是
$ 5 \sqrt { 2 } + 2 \sqrt { 3 } $
.
答案:
$ 5 \sqrt { 2 } + 2 \sqrt { 3 } $
17. (6分)计算:
(2)$(2\sqrt{48}-3\sqrt{27})÷\sqrt{6}$
(2)$(2\sqrt{48}-3\sqrt{27})÷\sqrt{6}$
$-\frac{\sqrt{2}}{2}$
.
答案:
【解析】:
### $(1)$计算$(\sqrt{48}-4\sqrt{\frac{1}{8}})-(3\sqrt{\frac{1}{3}} - 2\sqrt{0.5})$
**步骤一:化简各项根式**
根据根式化简公式$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}(a\geq0,b\geq0)$,$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}(a\geq0,b > 0)$对原式各项进行化简:
$\sqrt{48}=\sqrt{16×3}=4\sqrt{3}$;
$4\sqrt{\frac{1}{8}} = 4×\frac{\sqrt{1}}{\sqrt{8}}=4×\frac{1}{2\sqrt{2}}=\sqrt{2}$;
$3\sqrt{\frac{1}{3}} = 3×\frac{\sqrt{1}}{\sqrt{3}}=\sqrt{3}$;
$2\sqrt{0.5}=2\sqrt{\frac{1}{2}}=\sqrt{2}$。
**步骤二:代入化简后的根式进行计算**
将化简后的根式代入原式可得:
$(4\sqrt{3}-\sqrt{2})-(\sqrt{3}-\sqrt{2})$
去括号得:$4\sqrt{3}-\sqrt{2}-\sqrt{3}+\sqrt{2}$
合并同类二次根式:$(4\sqrt{3}-\sqrt{3})+(-\sqrt{2}+\sqrt{2}) = 3\sqrt{3}$。
### $(2)$计算$(2\sqrt{48}-3\sqrt{27})÷\sqrt{6}$
**步骤一:化简括号内的根式**
$\sqrt{48}=\sqrt{16×3}=4\sqrt{3}$,则$2\sqrt{48}=2×4\sqrt{3}=8\sqrt{3}$;
$\sqrt{27}=\sqrt{9×3}=3\sqrt{3}$,则$3\sqrt{27}=3×3\sqrt{3}=9\sqrt{3}$。
**步骤二:计算括号内的值**
$2\sqrt{48}-3\sqrt{27}=8\sqrt{3}-9\sqrt{3}=-\sqrt{3}$。
**步骤三:计算除法**
$(-\sqrt{3})÷\sqrt{6}=-\frac{\sqrt{3}}{\sqrt{6}}$,分母有理化,分子分母同时乘以$\sqrt{6}$得:
$-\frac{\sqrt{3}×\sqrt{6}}{\sqrt{6}×\sqrt{6}}=-\frac{\sqrt{18}}{6}=-\frac{3\sqrt{2}}{6}=-\frac{\sqrt{2}}{2}$。
【答案】:
$(1)$$\boldsymbol{3\sqrt{3}}$;$(2)$$\boldsymbol{-\frac{\sqrt{2}}{2}}$
### $(1)$计算$(\sqrt{48}-4\sqrt{\frac{1}{8}})-(3\sqrt{\frac{1}{3}} - 2\sqrt{0.5})$
**步骤一:化简各项根式**
根据根式化简公式$\sqrt{ab}=\sqrt{a}\cdot\sqrt{b}(a\geq0,b\geq0)$,$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}(a\geq0,b > 0)$对原式各项进行化简:
$\sqrt{48}=\sqrt{16×3}=4\sqrt{3}$;
$4\sqrt{\frac{1}{8}} = 4×\frac{\sqrt{1}}{\sqrt{8}}=4×\frac{1}{2\sqrt{2}}=\sqrt{2}$;
$3\sqrt{\frac{1}{3}} = 3×\frac{\sqrt{1}}{\sqrt{3}}=\sqrt{3}$;
$2\sqrt{0.5}=2\sqrt{\frac{1}{2}}=\sqrt{2}$。
**步骤二:代入化简后的根式进行计算**
将化简后的根式代入原式可得:
$(4\sqrt{3}-\sqrt{2})-(\sqrt{3}-\sqrt{2})$
去括号得:$4\sqrt{3}-\sqrt{2}-\sqrt{3}+\sqrt{2}$
合并同类二次根式:$(4\sqrt{3}-\sqrt{3})+(-\sqrt{2}+\sqrt{2}) = 3\sqrt{3}$。
### $(2)$计算$(2\sqrt{48}-3\sqrt{27})÷\sqrt{6}$
**步骤一:化简括号内的根式**
$\sqrt{48}=\sqrt{16×3}=4\sqrt{3}$,则$2\sqrt{48}=2×4\sqrt{3}=8\sqrt{3}$;
$\sqrt{27}=\sqrt{9×3}=3\sqrt{3}$,则$3\sqrt{27}=3×3\sqrt{3}=9\sqrt{3}$。
**步骤二:计算括号内的值**
$2\sqrt{48}-3\sqrt{27}=8\sqrt{3}-9\sqrt{3}=-\sqrt{3}$。
**步骤三:计算除法**
$(-\sqrt{3})÷\sqrt{6}=-\frac{\sqrt{3}}{\sqrt{6}}$,分母有理化,分子分母同时乘以$\sqrt{6}$得:
$-\frac{\sqrt{3}×\sqrt{6}}{\sqrt{6}×\sqrt{6}}=-\frac{\sqrt{18}}{6}=-\frac{3\sqrt{2}}{6}=-\frac{\sqrt{2}}{2}$。
【答案】:
$(1)$$\boldsymbol{3\sqrt{3}}$;$(2)$$\boldsymbol{-\frac{\sqrt{2}}{2}}$
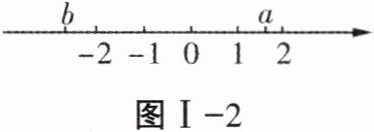
18. (6分)已知$a,b$在数轴上的位置如图Ⅰ-2所示:
化简:
$\sqrt{(a + 2)^2}-\sqrt{(b - 2)^2}+\sqrt{(a + b)^2}$=

化简:
$\sqrt{(a + 2)^2}-\sqrt{(b - 2)^2}+\sqrt{(a + b)^2}$=
0
答案:
【解析】:
本题可先根据$a$、$b$在数轴上的位置判断出$a + 2$、$b - 2$、$a + b$的正负性,再根据二次根式的性质$\sqrt{x^2}=\vert x\vert=\begin{cases}x(x\geq0)\\-x(x\lt0)\end{cases}$进行化简。
### 步骤一:判断$a + 2$、$b - 2$、$a + b$的正负性
由数轴可知$1\lt a\lt2$,$b\lt - 2$。
对于$a + 2$:因为$1\lt a\lt2$,所以$a + 2\gt0$。
对于$b - 2$:因为$b\lt - 2$,所以$b - 2\lt0$。
对于$a + b$:因为$1\lt a\lt2$,$b\lt - 2$,所以$\vert b\vert\gt\vert a\vert$,则$a + b\lt0$。
### 步骤二:根据二次根式的性质化简原式
根据二次根式的性质$\sqrt{x^2}=\vert x\vert$,对原式进行化简:
$\sqrt{(a + 2)^2}-\sqrt{(b - 2)^2}+\sqrt{(a + b)^2}=\vert a + 2\vert-\vert b - 2\vert+\vert a + b\vert$
因为$a + 2\gt0$,所以$\vert a + 2\vert=a + 2$;
因为$b - 2\lt0$,所以$\vert b - 2\vert=-(b - 2)=2 - b$;
因为$a + b\lt0$,所以$\vert a + b\vert=-(a + b)=-a - b$。
将上述化简结果代入原式可得:
$\begin{aligned}\vert a + 2\vert-\vert b - 2\vert+\vert a + b\vert&=(a + 2)-(2 - b)+(-a - b)\\&=a + 2 - 2 + b - a - b\\&=(a - a)+(b - b)+(2 - 2)\\&=0\end{aligned}$
【答案】:$\boldsymbol{0}$
本题可先根据$a$、$b$在数轴上的位置判断出$a + 2$、$b - 2$、$a + b$的正负性,再根据二次根式的性质$\sqrt{x^2}=\vert x\vert=\begin{cases}x(x\geq0)\\-x(x\lt0)\end{cases}$进行化简。
### 步骤一:判断$a + 2$、$b - 2$、$a + b$的正负性
由数轴可知$1\lt a\lt2$,$b\lt - 2$。
对于$a + 2$:因为$1\lt a\lt2$,所以$a + 2\gt0$。
对于$b - 2$:因为$b\lt - 2$,所以$b - 2\lt0$。
对于$a + b$:因为$1\lt a\lt2$,$b\lt - 2$,所以$\vert b\vert\gt\vert a\vert$,则$a + b\lt0$。
### 步骤二:根据二次根式的性质化简原式
根据二次根式的性质$\sqrt{x^2}=\vert x\vert$,对原式进行化简:
$\sqrt{(a + 2)^2}-\sqrt{(b - 2)^2}+\sqrt{(a + b)^2}=\vert a + 2\vert-\vert b - 2\vert+\vert a + b\vert$
因为$a + 2\gt0$,所以$\vert a + 2\vert=a + 2$;
因为$b - 2\lt0$,所以$\vert b - 2\vert=-(b - 2)=2 - b$;
因为$a + b\lt0$,所以$\vert a + b\vert=-(a + b)=-a - b$。
将上述化简结果代入原式可得:
$\begin{aligned}\vert a + 2\vert-\vert b - 2\vert+\vert a + b\vert&=(a + 2)-(2 - b)+(-a - b)\\&=a + 2 - 2 + b - a - b\\&=(a - a)+(b - b)+(2 - 2)\\&=0\end{aligned}$
【答案】:$\boldsymbol{0}$
查看更多完整答案,请扫码查看


