1. 下列图形中,一定可以拼成平行四边形的是(
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形
D
)A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形
答案:
D
2. 在$□ ABCD$中,延长$AB到E$,使$BE= AB$,连接$DE$,交$BC点F$,如图3-10所示,则下列结论不一定成立的是(
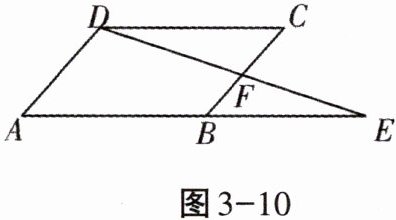
A.$\angle E= \angle CDF$
B.$EF= DF$
C.$AD= 2BF$
D.$BE= 2CF$
D
)
A.$\angle E= \angle CDF$
B.$EF= DF$
C.$AD= 2BF$
D.$BE= 2CF$
答案:
D
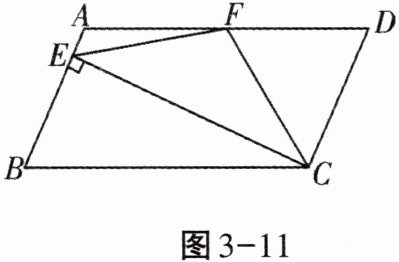
3. 如图3-11,在$□ ABCD$中,$AD= 2AB$,$F是AD$的中点,作$CE\perp AB$,垂足$E在线段AB$上,连接$EF$,$CF$,则下列结论中一定成立的是______
①$\angle DCF= \frac{1}{2}\angle BCD$;②$EF= CF$;
③$S_{\triangle BEC}= 2S_{\triangle CEF}$;④$\angle DFE= 3\angle AEF$。
①②④
。(写出所有正确结论的序号)①$\angle DCF= \frac{1}{2}\angle BCD$;②$EF= CF$;
③$S_{\triangle BEC}= 2S_{\triangle CEF}$;④$\angle DFE= 3\angle AEF$。

答案:
①②④
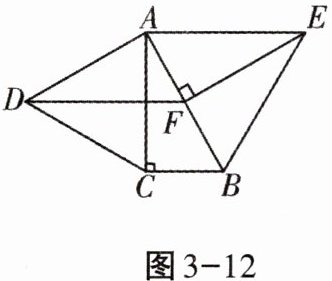
4. 如图3-12,分别以$Rt\triangle ABC的直角边AC及斜边AB为边向外作等边三角形ACD$、等边三角形$ABE$,过点$E作EF\perp AB$,垂足为$F$,连接$DF$,当$\frac{AC}{AB}= $
$\frac{\sqrt{3}}{2}$
时,四边形$ADFE$是平行四边形。
答案:
$\frac{\sqrt{3}}{2}$
5. 如图3-13,在$□ ABCD$中,$\angle BAC= 90^{\circ}$,$\angle ABC= 60^{\circ}$,$AB= 6$。动点$P从点A出发沿AD以1\mathrm{cm}/s速度向终点D$运动,同时点$Q从点C$出发,以$4\mathrm{cm}/s速度沿射线CB$运动,当点$P$到达终点时,点$Q$也随之停止运动,设点$P运动的时间为t\mathrm{s}$。
(1)用含$t的代数式表示BQ= $
(2)当$PQ\perp BC$时,求$t$的值。
(1)用含$t的代数式表示BQ= $
12 - 4t(0≤t≤3)或4t - 12(3<t≤12)
;(2)当$PQ\perp BC$时,求$t$的值。
$\frac{9}{5}$
答案:
(1)BQ=12 - 4t(0≤t≤3)或BQ=4t - 12(3<t≤12)
(2)$\frac{9}{5}$
(1)BQ=12 - 4t(0≤t≤3)或BQ=4t - 12(3<t≤12)
(2)$\frac{9}{5}$
查看更多完整答案,请扫码查看


