《2025年暑假作业兰州大学出版社八年级数学人教版》

16. (10分)如图4-32,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG,垂足为E,BF//DE交AG于F,探究线段AF,BF,EF三者之间的数量关系,并说明理由.
解:线段AF,BF,EF三者之间的数量关系为AF=BF+EF,理由如下:
　　　∵四边形ABCD是正方形，
　　　∴AB=AD,∠DAB=∠ABC=90°.
　　　∵DE⊥AG,垂足为E,BF// DE交AG于F,
　　　∴∠AED=∠DEF=∠AFB=90°,
　　　∴∠ADE+∠DAE=90°,∠DAE+∠BAF=90°,
　　　∴∠ADE=∠BAF.
　　　在△ABF和△DAE中,$\left\{\begin{array}{l}\angle BAF=\angle ADE,\\ \angle AFB=\angle DEA,\\ AB=AD,\end{array}\right.$
　　　∴△ABF≌△DAE(AAS),∴BF=AE,
　　　∴AF=AE+EF=BF+EF.

答案： 解:线段$AF$,$BF$,$EF$三者之间的数量关系为$AF=BF+EF$,理由如下:
　　　$\because$四边形$ABCD$是正方形，
　　　$\therefore AB=AD$,$\angle DAB=\angle ABC=90^{\circ}$.
　　　$\because DE\perp AG$,垂足为$E$,$BF// DE$交$AG$于$F$,
　　　$\therefore \angle AED=\angle DEF=\angle AFB=90^{\circ}$,
　　　$\therefore \angle ADE+\angle DAE=90^{\circ}$,$\angle DAE+\angle BAF=90^{\circ}$,
　　　$\therefore \angle ADE=\angle BAF$.
　　　在$\triangle ABF$和$\triangle DAE$中,$\left\{\begin{array}{l}\angle BAF=\angle ADE,\\ \angle AFB=\angle DEA,\\ AB=AD,\end{array}\right.$
　　　$\therefore \triangle ABF\cong \triangle DAE(AAS)$,$\therefore BF=AE$,
　　　$\therefore AF=AE+EF=BF+EF$.

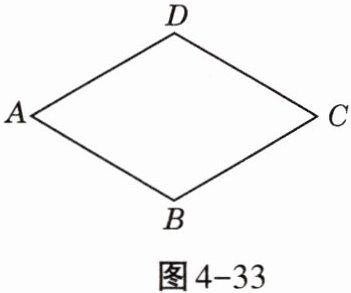
17. (12分)如图4-33,在菱形ABCD中,∠A与∠B的度数比为1:2,它的周长是48cm.
求：(1)两条对角线的长度；
(2)菱形ABCD的面积.

答案：
解:
(1)连接$AC$,$BD$,交于点$O$,如答图4-1,菱形$ABCD$的周长是$48cm$，
　　　　　　　
　　　则$AB=BC=CD=AD=12cm$.
　　　$\because \angle A:\angle B=1:2$,$\therefore \angle A=60^{\circ}$,$\angle B=120^{\circ}$,
　　　$\therefore \triangle ADB$是等边三角形,$AD=BD=12cm$,
　　　在$Rt\triangle ADO$中,$AO=\sqrt{AD^{2}-DO^{2}}=6\sqrt{3}cm$,
　　　$\therefore AC=2AO=12\sqrt{3}cm$.
(2)$S_{菱形ABCD}=\frac{1}{2}AC\cdot BD=72\sqrt{3}cm^{2}$.

18. (12分)如图4-34,在△ABC中,AB= AC,AD为∠BAC的平分线,AN为△ABC的外角∠BAM的平分线,BE⊥AN,垂足为点E.
(1)求证：四边形ADBE是矩形.
(2)连接DE,试判断四边形ACDE的形状,并证明你的结论.
证明:
　　　　(1)∵AD平分∠BAC,AN平分∠BAM,
　　　　∴∠BAD=1/2∠BAC,∠BAN=1/2∠BAM,
　　　　∴∠DAE=∠BAD+∠BAN=1/2(∠BAC+∠BAM)=1/2× 180°=90°,
　　　　∵AB=AC,AD平分∠BAC,
　　　　∴AD⊥BC,∴∠ADB=90°,
　　　　∵BE⊥AN,∴∠BEA=90°,
　　　　∴四边形ADBE是矩形.
　　　(2)四边形ACDE是平行四边形.
　　　证明:∵四边形ADBE是矩形，
　　　∴AE// BD,AE=BD.
　　　∵AB=AC,AD平分∠BAC,
　　　∴BD=CD,∴AE// CD,AE=CD,
　　　∴四边形ACDE是平行四边形.

答案： 证明:
(1)$\because AD$平分$\angle BAC$,$AN$平分$\angle BAM$,
　　　　$\therefore \angle BAD=\frac{1}{2}\angle BAC$,$\angle BAN=\frac{1}{2}\angle BAM$,
　　　　$\therefore \angle DAE=\angle BAD+\angle BAN=\frac{1}{2}(\angle BAC+\angle BAM)=\frac{1}{2}× 180^{\circ}=90^{\circ}$,
　　　　$\because AB=AC$,$AD$平分$\angle BAC$,
　　　　$\therefore AD\perp BC$,$\therefore \angle ADB=90^{\circ}$,
　　　　$\because BE\perp AN$,$\therefore \angle BEA=90^{\circ}$,
　　　　$\therefore$四边形$ADBE$是矩形.
(2)四边形$ACDE$是平行四边形.
　　　证明:$\because$四边形$ADBE$是矩形，
　　　$\therefore AE// BD$,$AE=BD$.
　　　$\because AB=AC$,$AD$平分$\angle BAC$,
　　　$\therefore BD=CD$,$\therefore AE// CD$,$AE=CD$,
　　　$\therefore$四边形$ACDE$是平行四边形.

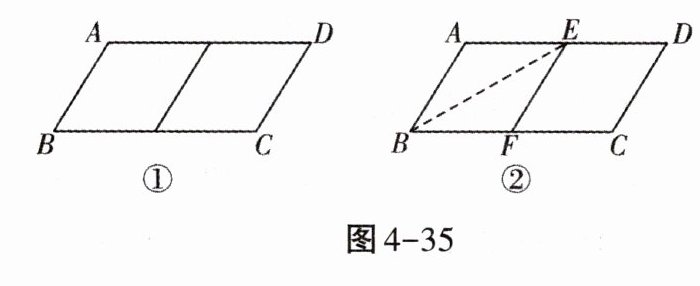
19. (14分)邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作；在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作……依次类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图4-35①,在□ABCD中,若AB= 1,BC= 2,则□ABCD为1阶准菱形.
(1)猜想与计算
邻边长分别为3和5的平行四边形是___阶准菱形；已知□ABCD的邻边长分别为a,b(a＞b),满足a= 8b+r,b= 5r,请写出□ABCD是______阶准菱形.
(2)操作与推理
小明为了剪去一个菱形,进行如下操作：如图4-35②,把□ABCD沿BE折叠(点E在AD上),使点A落在边BC上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.

答案：

(1)解:如答图4-2,
　　　　　　　　
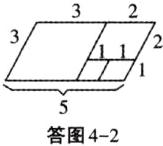
　　利用邻边长分别为3和5的平行四边形进行3次操作，所剩四边形是边长为1的菱形，故邻边长分别为3和5的平行四边形是3阶准菱形;
　　如答图4-3,
　　　　
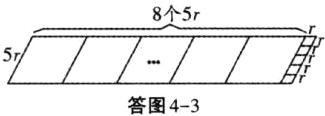
　　$\because b=5r$,$\therefore a=8b+r=40r+r=8× 5r+r$,
　　利用邻边长分别为$41r$和$5r$的平行四边形进行$8+4=12$次操作，所剩四边形是边长为$r$的菱形，故邻边长分别为$41r$和$5r$的平行四边形是12阶准菱形.故答案为:3,12.
(2)证明:由折叠知:$\angle ABE=\angle FBE$,$AB=BF$,
　　$\because$四边形$ABCD$是平行四边形，$\therefore AE// BF$,
　　$\therefore \angle AEB=\angle FBE$,$\therefore \angle AEB=\angle ABE$,
　　$\therefore AE=AB$,$\therefore AE=BF$,
　　$\therefore$四边形$ABFE$是平行四边形，
　　$\therefore$四边形$ABFE$是菱形.