《2025年暑假作业兰州大学出版社八年级数学人教版》

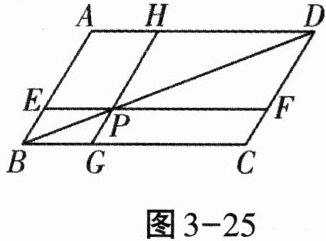
14. 如图3-25,在$□ ABCD$中,过对角线$BD上一点P作EF// BC$,$GH// AB$,且$CG= 2BG$,$S_{\triangle BPG}= 1$,则$S_{□ AEPH}= $4。

答案： 4

15. (10分)已知：如图3-26,$E$,$F为□ ABCD对角线AC$上的两点,且$AE= CF$,连接$BE$,$DF$,求证：$BE= DF$。
证明:∵四边形ABCD是平行四边形，
∴AB//DC,AB=DC,∴∠BAE=∠DCF.
在△AEB和△CFD中,
$\left\{\begin{array}{l} AB=CD,\\ ∠BAE=∠DCF,\\ AE=CF,\end{array}\right.$
∴△AEB≌△CFD(SAS),∴BE=DF.

答案： 证明:
∵四边形ABCD是平行四边形，
∴AB//DC,AB=DC,
∴∠BAE=∠DCF.
在△AEB和△CFD中,
$\left\{\begin{array}{l} AB=CD,\\ ∠BAE=∠DCF,\\ AE=CF,\end{array}\right.$
∴△AEB≌△CFD(SAS),
∴BE=DF.

16. (12分)如图3-27,在四边形$ABCD$中,$AC$,$BD相交于点O$,$O是AC$的中点,$AD// BC$,$AC= 8$,$BD= 6$。
(1)求证：四边形$ABCD$是平行四边形；
证明:∵O是AC的中点，
∴OA=OC.∵AD//BC,∴∠ADO=∠CBO.
在△AOD和△COB中,
$\left\{\begin{array}{l} ∠ADO=∠CBO,\\ ∠AOD=∠COB,\\ OA=OC,\end{array}\right.$
∴△AOD≌△COB,∴OD=OB,
∴四边形ABCD是平行四边形.
(2)若$AC\perp BD$,求$□ ABCD$的面积。
解:∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,∴$S_{□ABCD}=$$\frac{1}{2}AC\cdot BD$=24.

答案：
(1)证明:
∵O是AC的中点，
∴OA=OC.
∵AD//BC,
∴∠ADO=∠CBO.
在△AOD和△COB中,
$\left\{\begin{array}{l} ∠ADO=∠CBO,\\ ∠AOD=∠COB,\\ OA=OC,\end{array}\right.$
∴△AOD≌△COB,
∴OD=OB,
∴四边形ABCD是平行四边形.
(2)解:
∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
∴$S_{□ABCD}=\frac{1}{2}AC\cdot BD=24$.

17. (12分)(1)回归课本
请用文字语言表述三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半。
(2)回顾证法
证明三角形中位线定理的方法很多,但多数都要通过添加辅助线构图完成。下面是其中一种辅助线的添加方法。请结合图3-28(2),补全求证及证明过程。
已知：如图3-28(1),在$\triangle ABC$中,点$D$,$E分别是AB$,$AC$的中点。
求证：DE平行于BC，且DE等于BC的一半。
证明：过点$C作CF// AB$,与$DE的延长线交于点F$。
(3)实践应用
如图3-28(3),点$B和点C$被池塘隔开,在$BC外选一点A$,连接$AB$,$AC$,分别取$AB$,$AC的中点D$,$E$,测得$DE的长度为9\mathrm{m}$,则$B$,$C$两点间的距离为18m。

答案：
(1)证明:
∵四边形ABCD是平行四边形,
∴DC=AB,DC//AB,
∴∠ODF=∠OBE.
在△ODF与△OBE中,
$\left\{\begin{array}{l} ∠ODF=∠OBE,\\ ∠DOF=∠BOE,\\ DF=BE,\end{array}\right.$
∴△ODF≌△OBE(AAS),
∴BO=DO.
(2)解:
∵BD⊥AD,
∴∠ADB=90°.
∵∠A=45°,
∴∠DBA=∠A=45°.
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形.
∵AB//CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∴DF=FG=1,
∴DG=$\sqrt{DF^{2}+FG^{2}}=\sqrt{2}$.
∵DG=DO=$\sqrt{2}$,又
∵DO=BO,
∴AD=2DO=2$\sqrt{2}$.