10. 如图2-5所示,$\angle C = \angle ABD = 90^{\circ}$,$AC = 4$,$BC = 3$,$BD = 12$,则$AD = $
13
.
答案:
13
11. 如图2-6所示,已知一根长8m的竹竿在离地3m处($A$点)断裂,竹竿顶部($B$点)抵着地面,此时,顶部距底部的距离($BC$的长)为多少?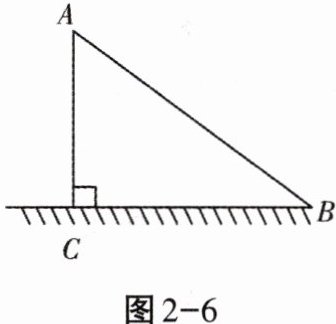
解:$\because AC=3,AB=8 - 3 = 5$,
$\therefore BC=\sqrt{5^{2}-3^{2}} = $

解:$\because AC=3,AB=8 - 3 = 5$,
$\therefore BC=\sqrt{5^{2}-3^{2}} = $
4
$(m)$.$\therefore BC$的长为4m.
答案:
解:$\because AC=3,AB=8 - 3 = 5$,
$\therefore BC=\sqrt{5^{2}-3^{2}} = 4(m)$.$\therefore BC$的长为4m.
$\therefore BC=\sqrt{5^{2}-3^{2}} = 4(m)$.$\therefore BC$的长为4m.
12. 如图2-7所示,为修通铁路凿通隧道$AC$,量出$\angle C = 90^{\circ}$,$AB = 5km$,$BC = 4km$,若每天凿隧道0.3km,问几天才能把隧道$AC$凿通?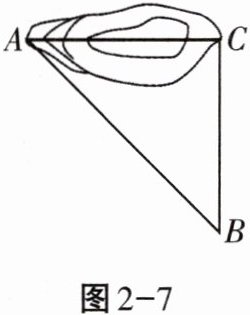
解:在$Rt\triangle ABC$中,$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5^{2}-4^{2}} = $

解:在$Rt\triangle ABC$中,$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5^{2}-4^{2}} = $
3
$(km)$,$\because \frac{3}{0.3}=$10
(天),$\therefore $10
天能将隧道$AC$凿通.
答案:
解:在$Rt\triangle ABC$中,$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{5^{2}-4^{2}} = 3(km)$,$\because \frac{3}{0.3}=10$(天),
$\therefore 10$天能将隧道$AC$凿通.
$\therefore 10$天能将隧道$AC$凿通.
13. 如图2-8所示,在笔直的高速路旁边有$A$,$B$两个村庄,$A村庄到公路的距离AC = 8km$,$B村庄到公路的距离BD = 14km$,测得$C$,$D$两点的距离为20km,现要在$CD之间建一个服务区E$,使得$A$,$B两村庄到服务区E$的距离相等,求$CE$的长.
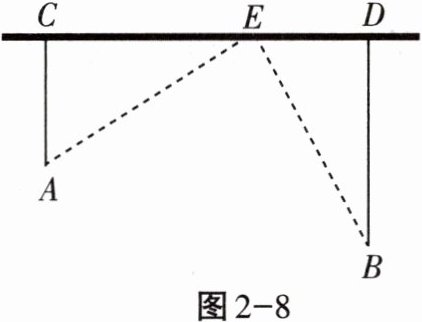
解:设$CE = xkm$,则$DE=(20 - x)km$.
在$Rt\triangle ACE$中,由勾股定理得:
$AE^{2}=AC^{2}+CE^{2}=8^{2}+x^{2}$,
在$Rt\triangle BDE$中,由勾股定理得:
$BE^{2}=BD^{2}+DE^{2}=14^{2}+(20 - x)^{2}$,
由题意可知:$AE = BE$,
所以:$8^{2}+x^{2}=14^{2}+(20 - x)^{2}$,解得:$x = $
所以$CE = $

解:设$CE = xkm$,则$DE=(20 - x)km$.
在$Rt\triangle ACE$中,由勾股定理得:
$AE^{2}=AC^{2}+CE^{2}=8^{2}+x^{2}$,
在$Rt\triangle BDE$中,由勾股定理得:
$BE^{2}=BD^{2}+DE^{2}=14^{2}+(20 - x)^{2}$,
由题意可知:$AE = BE$,
所以:$8^{2}+x^{2}=14^{2}+(20 - x)^{2}$,解得:$x = $
13.3
,所以$CE = $
13.3
$km$.
答案:
解:设$CE = xkm$,则$DE=(20 - x)km$.
在$Rt\triangle ACE$中,由勾股定理得:
$AE^{2}=AC^{2}+CE^{2}=8^{2}+x^{2}$,
在$Rt\triangle BDE$中,由勾股定理得:
$BE^{2}=BD^{2}+DE^{2}=14^{2}+(20 - x)^{2}$,
由题意可知:$AE = BE$,
所以:$8^{2}+x^{2}=14^{2}+(20 - x)^{2}$,解得:$x = 13.3$,
所以$CE = 13.3km$.
在$Rt\triangle ACE$中,由勾股定理得:
$AE^{2}=AC^{2}+CE^{2}=8^{2}+x^{2}$,
在$Rt\triangle BDE$中,由勾股定理得:
$BE^{2}=BD^{2}+DE^{2}=14^{2}+(20 - x)^{2}$,
由题意可知:$AE = BE$,
所以:$8^{2}+x^{2}=14^{2}+(20 - x)^{2}$,解得:$x = 13.3$,
所以$CE = 13.3km$.
1. 如图2-9所示,每个小正方形的边长为1,$A$,$B$,$C$是小正方形的顶点,则$\angle ABC$的度数为(
A.$90^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$30^{\circ}$
C
)A.$90^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$30^{\circ}$
答案:
C
2. 如图2-10,四边形$OABC$为正方形,边长为6,点$A$,$C分别在x$轴、$y$轴的正半轴上,点$D在OA$上,且$D点的坐标为(2,0)$,$P是OB$上的一个动点,$PD + PA$的最小值是( )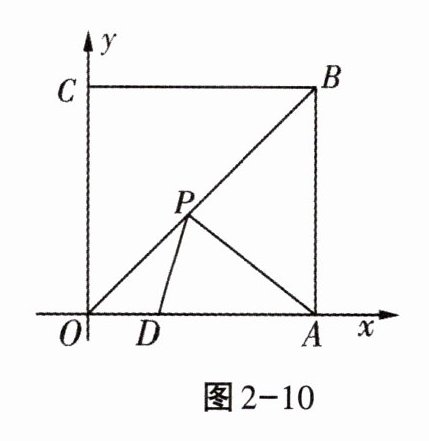
A.$2\sqrt{10}$
B.$\sqrt{10}$
C.4
D.6

A.$2\sqrt{10}$
B.$\sqrt{10}$
C.4
D.6
答案:
A 解析:
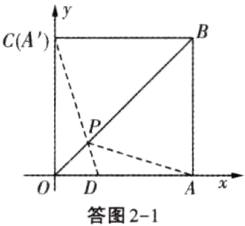
如答图2-1,作$A$点关于$OB$的对称点$A'$,$\because$四边形$OABC$为正方形.
$\therefore A'$与$C$重合,$CD$为所求最小值,$CD=\sqrt{6^{2}+2^{2}} = 2\sqrt{10}$.
A 解析:

如答图2-1,作$A$点关于$OB$的对称点$A'$,$\because$四边形$OABC$为正方形.
$\therefore A'$与$C$重合,$CD$为所求最小值,$CD=\sqrt{6^{2}+2^{2}} = 2\sqrt{10}$.
查看更多完整答案,请扫码查看


