《2025年暑假作业兰州大学出版社八年级数学人教版》

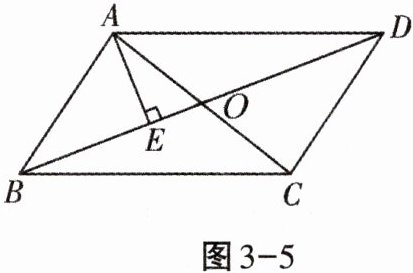
9. 如图3-5,在$□ ABCD$中,$AE\perp BD$,垂足为$E$,$\angle EAC= 30^{\circ}$,$AE= 3$,则$AC$的长为4√3。

答案： 4√3

10. 如图3-6,在$□ ABCD$中,$AB= \sqrt{13}$,$AD= 4$,将$□ ABCD沿AE$翻折后,点$B恰好与点C$重合,则折痕$AE$的长为3。

答案： 3

11. 如图3-7,在四边形$ABCD$中,对角线$AC$,$BD相交于点E$,$\angle CBD= 90^{\circ}$,$BC= 4$,$BE= ED= 3$,$AC= 10$,则四边形$ABCD$的面积为______24。

答案： 24

12. 如图3-8,在四边形$ABCD$中,$AB// CD$,$E$,$F为对角线AC$上两点,且$AE= CF$,$DF// BE$。
求证：四边形$ABCD$为平行四边形。
证明:∵AB//CD,
∴∠DCA=∠BAC.∵DF//BE,
∴∠DFA=∠BEC,∴∠AEB=∠DFC.
在△AEB和△CFD中,
$\left\{\begin{array}{l} ∠DCF=∠EAB,\\ AE=CF,\\ ∠DFC=∠AEB,\end{array}\right.$
∴△AEB≌△CFD(ASA),
∴AB=CD.∵AB//CD,
∴四边形ABCD为平行四边形.

答案： 证明:
∵AB//CD,
∴∠DCA=∠BAC.
∵DF//BE,
∴∠DFA=∠BEC,
∴∠AEB=∠DFC.
在△AEB和△CFD中,
$\left\{\begin{array}{l} ∠DCF=∠EAB,\\ AE=CF,\\ ∠DFC=∠AEB,\end{array}\right.$
∴△AEB≌△CFD(ASA),
∴AB=CD.
∵AB//CD,
∴四边形ABCD为平行四边形.

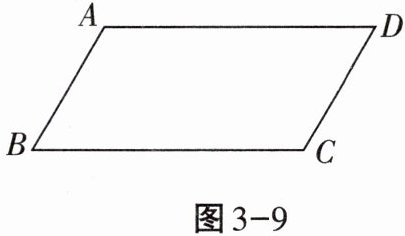
13. 如图3-9,已知四边形$ABCD$是平行四边形。
(1)尺规作图：作$\angle BCD的角平分线CE交AD于点E$(不要求写作法,但要保留作图痕迹)；
(2)在(1)所作图形中,求证：$DC= DE$。

答案：

(1)解:如答图3−1所示:CE即为所求;
(2)证明:
∵四边形ABCD是平行四边形，
∴AD//BC,
∴∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠DEC=∠DCE,
∴DE=DC.