《2025年暑假作业兰州大学出版社八年级数学人教版》

24. (10分)某公司为了让员工感受“绿色引领时尚”的理念,组织员工参观北京世界园艺博览会。这个公司联系了甲、乙两家旅行社,他们的报价均为280元/人,若参观人数不超过10人,均无优惠；若参观人数超过10人,甲旅行社将超出人员的费用按报价打八折,而乙旅行社将全体参观人员的费用按报价打九折。
现在该公司结合实际情况,想从甲、乙两家旅行社中选取一家承担这项参观业务。设该公司参观人数为$x(x ＞ 10)$,甲、乙两家旅行社收取的费用分别为$y_1$(元)和$y_2$(元)。
(1)分别求出$y_1和y_2与x$之间的函数关系式；
(2)假设两家旅行社除优惠方案不同外,其他服务基本相同。请问该公司选择哪家旅行社费用较低？

答案： 解:
(1)y₁=280×0.8(x-10)+280×10=224x+560(x＞10),
y₂=280×0.9x=252x(x＞10).
(2)y₁-y₂=-28x+560,令-28x+560=0,则x=20;
①当x＞20时,y₁＜y₂,选甲旅行社的费用较低;
②当x=20时,y₁=y₂,选甲、乙两家旅行社的费用相同;
③10＜x＜20时,y₁＞y₂,选乙旅行社的费用较低.

25. (12分)某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆$A、B$两种型号客车作为交通工具。下表是租车公司提供给学校有关两种型号客车的载客量和租金信息：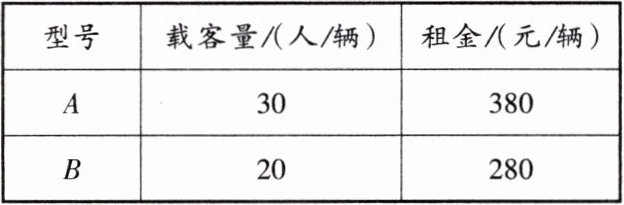
注：载客量指的是每辆客车最多可载该校师生的人数。
设学校租用$A型号客车x$辆,租车总费用为$y$元。
(1)求$y关于x$的函数解析式,并直接写出$x$的取值范围；
解：函数解析式为$y=$100x+17360，$x$的取值范围为21≤x≤62。
(2)若要使租车总费用不超过21940元,一共有几种租车方案？哪种租车方案最省钱？
解：一共有25种租车方案，租A型号客车21辆，B型号客车41辆最省钱。

答案： 解:
(1)由题意:y=380x+280(62-x)=100x+17360,
∵30x+20(62-x)≥1441,
∴x≥20.1,
∴x的取值范围为21≤x≤62.
(2)由题意得100x+17360≤21940,
∴x≤45.8.又
∵x≥20.1,
∴21≤x≤45,
∴共有25种租车方案.
∵y随x的增大而增大,
∴x=21时,y取最小值.
x=21时,y=100×21+17360=19460,即租A型号客车21辆,B型号客车41辆时最省钱,最少租车费为19460元.