《2025年暑假作业兰州大学出版社八年级数学人教版》

1. 如果直角三角形的三条边分别为4,5,a,那么a的值可以有 (C)
A.0个
B.1个
C.2个
D.3个

答案： C 解析：$a$ 可为直角边，也可为斜边。

2. 在$Rt△ABC$中,$∠C= 90^{\circ },AB= 10,AC:BC= 4:3,CD⊥AB$,垂足为D,则CD的长为 ($\frac{24}{5}$)
A.$\frac {24}{5}$
B.$\frac {12}{5}$
C.$\frac {6}{3}$
D.不能确定

答案： A 解析：设 $AC = 4x$，则 $BC = 3x$，由 $(4x)^2 + (3x)^2 = 10^2$，解得 $x = 2$，$\therefore AC = 8$，$BC = 6$，由 $AB \cdot CD = AC \cdot BC$，得 $CD = \frac{8 × 6}{10} = \frac{24}{5}$。

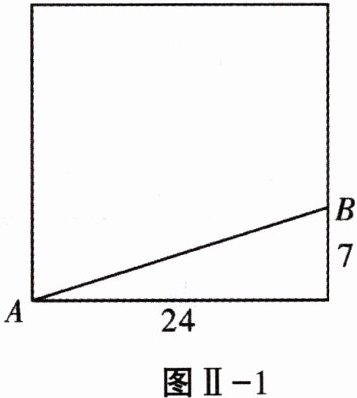
3. 如图Ⅱ-1,有一块边长为24m的正方形绿地,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处立一个标牌“少走6m,踏之何忍”,“□”中应填的数字是 ( )

A.3
B.4
C.5
D.6

答案： D 解析：由勾股定理可知 $AB = 25m$，即践踏绿地走 $25m$，原来需要走 $24 + 7 = 31(m)$，所以少走 $31 - 25 = 6(m)$。

4. 如图Ⅱ-2,已知四边形ABCD中,$AB= $ $3cm,AD= 4cm,BC= 13cm,CD= 12cm,且∠A= 90^{\circ }$,则四边形ABCD的面积为 (36cm²)
A.$12cm^{2}$
B.$36cm^{2}$
C.$22cm^{2}$
D.$18cm^{2}$

答案： B 解析：连接 $BD$，在 $Rt\triangle ABD$ 中，$\because AB = 3$，$AD = 4$，$\therefore BD = 5$，又 $CD = 12$，$BC = 13$，$\therefore \triangle BCD$ 是直角三角形，$\therefore S_{四边形ABCD} = S_{\triangle ABD} + S_{\triangle BCD} = \frac{1}{2} × 3 × 4 + \frac{1}{2} × 5 × 12 = 36(cm^2)$。

5. 如图Ⅱ-3,有一个池塘,其底面是边长为10尺的正方形,一个芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的$B'$.则这根芦苇的长度是 (D)
A.10尺
B.11尺
C.12尺
D.13尺

答案： D

6. 小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了5根火柴棒和12根火柴棒,那么他摆完这个直角三角形时共用火柴棒 (D)
A.13根
B.18根
C.25根
D.30根

答案： D