搜索
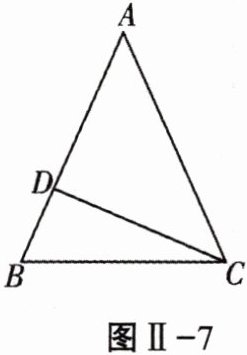
13. 如图Ⅱ-7,已知$△ABC$中,$AB= AC= $ $13,BC= 10$,若点D是边AB上的动点,则CD的最小值是____.
答案：
$\frac{120}{13}$ 解析：
过点 $A$ 作 $AE \perp BC$，垂足为 $E$，又 $AB = AC$，$\therefore E$ 是 $BC$ 的中点。$\because$ 在 $Rt\triangle ABE$ 中，有 $AE = \sqrt{AB^2 - BE^2} = \sqrt{13^2 - 5^2} = 12$，点 $D$ 在 $AB$ 上运动时，$CD$ 最短是当 $CD \perp AB$ 时，此时 $CD$ 是边 $AB$ 上的高，$\therefore S_{\triangle ABC} = \frac{1}{2} \cdot CD \cdot AB = \frac{1}{2} \cdot AE \cdot BC$，即 $CD = \frac{12 × 10}{13} = \frac{120}{13}$。
$\frac{120}{13}$ 解析：
过点 $A$ 作 $AE \perp BC$，垂足为 $E$，又 $AB = AC$，$\therefore E$ 是 $BC$ 的中点。$\because$ 在 $Rt\triangle ABE$ 中，有 $AE = \sqrt{AB^2 - BE^2} = \sqrt{13^2 - 5^2} = 12$，点 $D$ 在 $AB$ 上运动时，$CD$ 最短是当 $CD \perp AB$ 时，此时 $CD$ 是边 $AB$ 上的高，$\therefore S_{\triangle ABC} = \frac{1}{2} \cdot CD \cdot AB = \frac{1}{2} \cdot AE \cdot BC$，即 $CD = \frac{12 × 10}{13} = \frac{120}{13}$。 14. 图Ⅱ-8是著名的赵爽弦图,已知大正方形的面积是49,小正方形的面积是4.用a,b表示其中直角三角形的两条直角边$(a＞b)$,则2ab的值为____
45
.
答案：
45 解析：根据图形可得四个三角形的面积 + 小正方形的面积 = 大正方形的面积，即 $4 × \frac{1}{2}ab + 4 = 49$，得 $2ab + 4 = 49$，$\therefore 2ab = 49 - 4 = 45$。
15. 如图Ⅱ-9,$∠OAB= ∠OBC= ∠OCD= $ $90^{\circ }$,已知$OA= 4,AB= 1,BC= 2,CD= 3$,则$OD^{2}= $
30
.
答案：
30 解析：$OD^2 = OA^2 + AB^2 + BC^2 + CD^2 = 16 + 1 + 4 + 9 = 30$。
16. 若a,b,c为$△ABC$的三边长,且a,b,c满足$a^{2}+|b-15|+(c-17)^{2}+64= 16a$,则此三角形为____
直角三角形
.
答案：
直角三角形 解析：$\because a$，$b$，$c$ 满足 $a^2 + |b - 15| + (c - 17)^2 + 64 = 16a$，$\therefore a^2 - 16a + 64 + |b - 15| + (c - 17)^2 = 0$，即：$(a - 8)^2 + |b - 15| + (c - 17)^2 = 0$，由非负性可知：$a - 8 = 0$，$b - 15 = 0$，$c - 17 = 0$，$\therefore a = 8$，$b = 15$，$c = 17$。又 $\because a^2 + b^2 = 8^2 + 15^2 = 17^2 = c^2$，$\therefore \triangle ABC$ 是直角三角形。
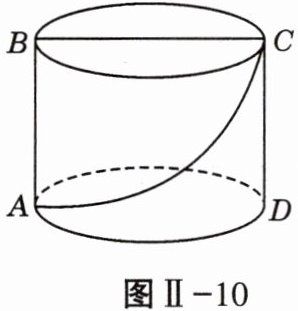
17. (6分)如图Ⅱ-10,一个圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出蚂蚁爬行的最短路程.
答案：
解：根据题意画出圆柱侧面展开图，连接 $AC$，
根据两点之间线段最短，蚂蚁从 $A$ 出发沿圆柱侧面爬行到 $C$ 的最短路程为 $AC$。$\because$ 圆柱的底面周长为 $20cm$，$\therefore BC = AD = 10cm$。又 $\because AB = 4cm$，$\therefore$ 在 $Rt\triangle ADC$ 中，$AC = \sqrt{AD^2 + DC^2} = 2\sqrt{29}$，则蚂蚁爬行的最短路程为 $2\sqrt{29}cm$。
解：根据题意画出圆柱侧面展开图，连接 $AC$，
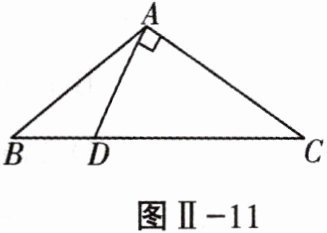
根据两点之间线段最短，蚂蚁从 $A$ 出发沿圆柱侧面爬行到 $C$ 的最短路程为 $AC$。$\because$ 圆柱的底面周长为 $20cm$，$\therefore BC = AD = 10cm$。又 $\because AB = 4cm$，$\therefore$ 在 $Rt\triangle ADC$ 中，$AC = \sqrt{AD^2 + DC^2} = 2\sqrt{29}$，则蚂蚁爬行的最短路程为 $2\sqrt{29}cm$。 18. (6分)如图Ⅱ-11,在$△ABC$中,已知$AB= AC= 20cm,BC= 32cm$,D是BC上一点,且$AD⊥AC$,求BD的长.
答案：
解：过点 $A$ 作 $AE \perp BC$，垂足为 $E$。
$\because AB = AC = 20$，$BC = 32$，$\therefore CE = BE = 16$，$\therefore$ 在 $Rt\triangle AEC$ 中，$AE = \sqrt{AC^2 - EC^2} = 12$。$\because AD \perp AC$，设 $DE = x$，$\therefore$ 在 $Rt\triangle ADC$ 中，有 $AD^2 = DC^2 - AC^2 = (x + 16)^2 - 20^2$，在 $Rt\triangle ADE$ 中，有 $AD^2 = DE^2 + AE^2 = x^2 + 12^2$，$\therefore (x + 16)^2 - 20^2 = x^2 + 12^2$，解得：$x = 9$，$\therefore BD = BE - DE = 16 - 9 = 7(cm)$。
解：过点 $A$ 作 $AE \perp BC$，垂足为 $E$。
$\because AB = AC = 20$，$BC = 32$，$\therefore CE = BE = 16$，$\therefore$ 在 $Rt\triangle AEC$ 中，$AE = \sqrt{AC^2 - EC^2} = 12$。$\because AD \perp AC$，设 $DE = x$，$\therefore$ 在 $Rt\triangle ADC$ 中，有 $AD^2 = DC^2 - AC^2 = (x + 16)^2 - 20^2$，在 $Rt\triangle ADE$ 中，有 $AD^2 = DE^2 + AE^2 = x^2 + 12^2$，$\therefore (x + 16)^2 - 20^2 = x^2 + 12^2$，解得：$x = 9$，$\therefore BD = BE - DE = 16 - 9 = 7(cm)$。 查看更多完整答案，请扫码查看
