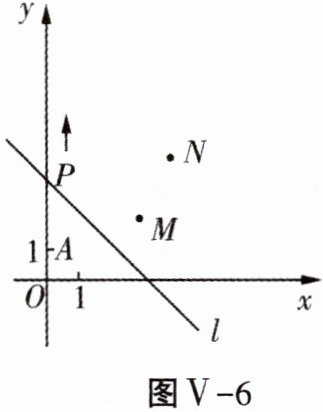
21. (6分)如图V-6,点$A,M,N的坐标分别为A(0,1)$,$M(3,2)$,$N(4,4)$,动点$P从点A$出发,沿$y$轴以每秒1个单位长度的速度向上移动,且过点$P的直线l:y = -x + b$也随之移动,设移动的时间为$t\ \text{s}$。
(1)当$t = 3$时,求直线$l$的解析式;
解:直线y=-x+b交y轴于点P(0,b),由题意,得b>0,t≥0,∵b=1+t,当t=3时,b=4.∴直线$l$的解析式为
(2)若点$M,N位于l$的异侧,确定$t$的取值范围。
解:当直线y=-x+b过点M(3,2)时,有2=-3+b,解得b=5.∵b=1+t,∴t=4.当直线y=-x+b过点N(4,4)时,有4=-4+b,解得b=8.∵b=1+t,∴t=7.故若点M,N位于l的异侧,t的取值范围是
(1)当$t = 3$时,求直线$l$的解析式;
解:直线y=-x+b交y轴于点P(0,b),由题意,得b>0,t≥0,∵b=1+t,当t=3时,b=4.∴直线$l$的解析式为
y=-x+4
。(2)若点$M,N位于l$的异侧,确定$t$的取值范围。
解:当直线y=-x+b过点M(3,2)时,有2=-3+b,解得b=5.∵b=1+t,∴t=4.当直线y=-x+b过点N(4,4)时,有4=-4+b,解得b=8.∵b=1+t,∴t=7.故若点M,N位于l的异侧,t的取值范围是
4<t<7
。
答案:
解:
(1)直线y=-x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,
∵b=1+t,当t=3时,b=4.
∴y=-x+4.
(2)当直线y=-x+b过点M(3,2)时,
有2=-3+b,解得b=5.
∵b=1+t,
∴t=4.
当直线y=-x+b过点N(4,4)时,
有4=-4+b,解得b=8.
∵b=1+t,
∴t=7.
故若点M,N位于l的异侧,t的取值范围是4<t<7.
(1)直线y=-x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,
∵b=1+t,当t=3时,b=4.
∴y=-x+4.
(2)当直线y=-x+b过点M(3,2)时,
有2=-3+b,解得b=5.
∵b=1+t,
∴t=4.
当直线y=-x+b过点N(4,4)时,
有4=-4+b,解得b=8.
∵b=1+t,
∴t=7.
故若点M,N位于l的异侧,t的取值范围是4<t<7.
22. (6分)(1)画出函数$y = |x - 1|$的图象。
(2)设$P(x,0)是x$轴上的一个动点,它与$x轴上表示-3的点的距离为y$。求$y关于x$的函数解析式,并画出这个函数的图象。
(2)设$P(x,0)是x$轴上的一个动点,它与$x轴上表示-3的点的距离为y$。求$y关于x$的函数解析式,并画出这个函数的图象。
答案:
解:
(1)由题意得:y=|x-1|,
即y=$\begin{cases}x - 1 & (x ≥ 1)\\-x + 1 & (x < 1)\end{cases}$
x 0 2
y=x - 1 1
x 0 1
y=-x + 1 1 0
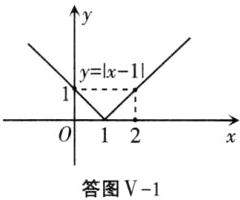
函数图象如答图V-1.
(2)由题意得:y=|x-(-3)|=|x+3|,即y=$\begin{cases}x + 3 & (x ≥ -3)\\-x - 3 & (x < -3)\end{cases}$
x -3 -2
y=x + 3 0 1
x -4 -3
y=-x - 3 1 0
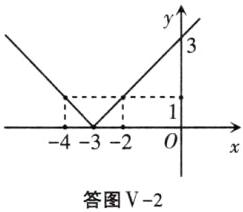
函数图象如答图V-2.
解:
(1)由题意得:y=|x-1|,
即y=$\begin{cases}x - 1 & (x ≥ 1)\\-x + 1 & (x < 1)\end{cases}$
x 0 2
y=x - 1 1
x 0 1
y=-x + 1 1 0

函数图象如答图V-1.
(2)由题意得:y=|x-(-3)|=|x+3|,即y=$\begin{cases}x + 3 & (x ≥ -3)\\-x - 3 & (x < -3)\end{cases}$
x -3 -2
y=x + 3 0 1
x -4 -3
y=-x - 3 1 0

函数图象如答图V-2.
23. (10分)一鱼池有一进水管和一出水管,出水管每小时可排出$5\ \text{m}^3$的水,进水管每小时可注入$3\ \text{m}^3$的水,现鱼池中约有$60\ \text{m}^3$的水。
(1)当进水管、出水管同时打开时,请写出鱼池中的水量$y(\text{m}^3)与打开的时间x(\text{h})$之间的函数关系式;
(2)根据实际情况,鱼池中的水量不得少于$40\ \text{m}^3$。如果管理人员在上午$8:00$同时打开两水管,那么最迟不得超过几时,就应关闭两水管?
(1)当进水管、出水管同时打开时,请写出鱼池中的水量$y(\text{m}^3)与打开的时间x(\text{h})$之间的函数关系式;
(2)根据实际情况,鱼池中的水量不得少于$40\ \text{m}^3$。如果管理人员在上午$8:00$同时打开两水管,那么最迟不得超过几时,就应关闭两水管?
答案:
解:
(1)由题意可知y=60-5x+3x.
∴y=60-2x(0<x≤30).
(2)根据题意得60-2x≥40,
∴x≤10.
∴最迟应在下午6:00关闭两水管.
(1)由题意可知y=60-5x+3x.
∴y=60-2x(0<x≤30).
(2)根据题意得60-2x≥40,
∴x≤10.
∴最迟应在下午6:00关闭两水管.
查看更多完整答案,请扫码查看


