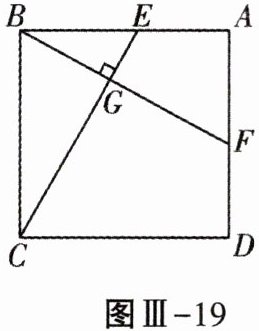
21. (8分)如图Ⅲ-19,四边形ABCD是正方形,E,F分别是边AB,AD上的一点,且$BF⊥CE$,垂足为G,求证:$AF= BE$.
证明:∵四边形$ ABCD $是正方形,
$ \therefore AB = BC $,$ \angle A = \angle CBE = 90^{\circ} $,∵$ BF \perp CE $,
$ \therefore \angle BCE + \angle CBG = 90^{\circ} $,$ \because \angle ABF + \angle CBG = 90^{\circ} $,
$ \therefore \angle BCE = \angle ABF $。
在$ \triangle BCE $和$ \triangle ABF $中,$ \left\{ \begin{array} { l } { \angle BCE = \angle ABF, } \\ { BC = AB, } \\ { \angle CBE = \angle A, } \end{array} \right. $
$ \therefore \triangle BCE \cong \triangle ABF ( $

证明:∵四边形$ ABCD $是正方形,
$ \therefore AB = BC $,$ \angle A = \angle CBE = 90^{\circ} $,∵$ BF \perp CE $,
$ \therefore \angle BCE + \angle CBG = 90^{\circ} $,$ \because \angle ABF + \angle CBG = 90^{\circ} $,
$ \therefore \angle BCE = \angle ABF $。
在$ \triangle BCE $和$ \triangle ABF $中,$ \left\{ \begin{array} { l } { \angle BCE = \angle ABF, } \\ { BC = AB, } \\ { \angle CBE = \angle A, } \end{array} \right. $
$ \therefore \triangle BCE \cong \triangle ABF ( $
ASA
$ ) $,$ \therefore BE = AF $。
答案:
证明:
∵四边形$ ABCD $是正方形,
$ \therefore AB = BC $,$ \angle A = \angle CBE = 90^{\circ} $,
∵$ BF \perp CE $,
$ \therefore \angle BCE + \angle CBG = 90^{\circ} $,$ \because \angle ABF + \angle CBG = 90^{\circ} $,
$ \therefore \angle BCE = \angle ABF $。
在$ \triangle BCE $和$ \triangle ABF $中,$ \left\{ \begin{array} { l } { \angle BCE = \angle ABF, } \\ { BC = AB, } \\ { \angle CBE = \angle A, } \end{array} \right. $
$ \therefore \triangle BCE \cong \triangle ABF ( ASA ) $,$ \therefore BE = AF $。
∵四边形$ ABCD $是正方形,
$ \therefore AB = BC $,$ \angle A = \angle CBE = 90^{\circ} $,
∵$ BF \perp CE $,
$ \therefore \angle BCE + \angle CBG = 90^{\circ} $,$ \because \angle ABF + \angle CBG = 90^{\circ} $,
$ \therefore \angle BCE = \angle ABF $。
在$ \triangle BCE $和$ \triangle ABF $中,$ \left\{ \begin{array} { l } { \angle BCE = \angle ABF, } \\ { BC = AB, } \\ { \angle CBE = \angle A, } \end{array} \right. $
$ \therefore \triangle BCE \cong \triangle ABF ( ASA ) $,$ \therefore BE = AF $。
22. (8分)如图Ⅲ-20,在矩形ABCD中,连接对角线AC,BD,将$\triangle ABC$沿BC方向平移,使点B移到点C,得到$\triangle DCE$.
(1)求证:$\triangle ACD\cong \triangle EDC$;
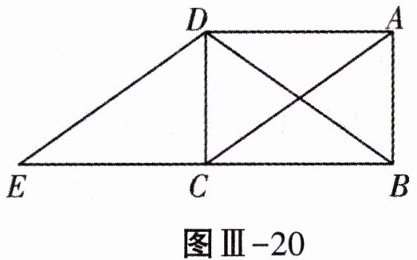
(2)请探究$\triangle BDE$的形状,并说明理由.
(1)求证:$\triangle ACD\cong \triangle EDC$;

证明:∵四边形$ ABCD $是矩形,$ \therefore AB = DC $,$ AC = BD $,$ AD = BC $,$ \angle ADC = \angle ABC = 90^{\circ} $。由平移的性质得:$ DE = AC $,$ CE = BC $,$ \angle DCE = \angle ABC = 90^{\circ} $,$ DC = AB $,$ \therefore AD = EC $。在$ \triangle ACD $和$ \triangle EDC $中,$ \left\{ \begin{array} { l } { AD = EC, } \\ { \angle ADC = \angle DCE, } \\ { CD = DC, } \end{array} \right. $$ \therefore \triangle ACD \cong \triangle EDC ( SAS ) $。
(2)请探究$\triangle BDE$的形状,并说明理由.
解:$ \triangle BDE $是等腰三角形,理由如下:$ \because AC = BD $,$ DE = AC $,$ \therefore BD = DE $,$ \therefore \triangle BDE $是等腰三角形。
答案:
(1) 证明:
∵四边形$ ABCD $是矩形,
$ \therefore AB = DC $,$ AC = BD $,$ AD = BC $,$ \angle ADC = \angle ABC = 90^{\circ} $。
由平移的性质得:$ DE = AC $,$ CE = BC $,$ \angle DCE = \angle ABC = 90^{\circ} $,$ DC = AB $,$ \therefore AD = EC $。
在$ \triangle ACD $和$ \triangle EDC $中,$ \left\{ \begin{array} { l } { AD = EC, } \\ { \angle ADC = \angle DCE, } \\ { CD = DC, } \end{array} \right. $
$ \therefore \triangle ACD \cong \triangle EDC ( SAS ) $。
(2) 解:$ \triangle BDE $是等腰三角形,理由如下:
$ \because AC = BD $,$ DE = AC $,$ \therefore BD = DE $,
$ \therefore \triangle BDE $是等腰三角形。
(1) 证明:
∵四边形$ ABCD $是矩形,
$ \therefore AB = DC $,$ AC = BD $,$ AD = BC $,$ \angle ADC = \angle ABC = 90^{\circ} $。
由平移的性质得:$ DE = AC $,$ CE = BC $,$ \angle DCE = \angle ABC = 90^{\circ} $,$ DC = AB $,$ \therefore AD = EC $。
在$ \triangle ACD $和$ \triangle EDC $中,$ \left\{ \begin{array} { l } { AD = EC, } \\ { \angle ADC = \angle DCE, } \\ { CD = DC, } \end{array} \right. $
$ \therefore \triangle ACD \cong \triangle EDC ( SAS ) $。
(2) 解:$ \triangle BDE $是等腰三角形,理由如下:
$ \because AC = BD $,$ DE = AC $,$ \therefore BD = DE $,
$ \therefore \triangle BDE $是等腰三角形。
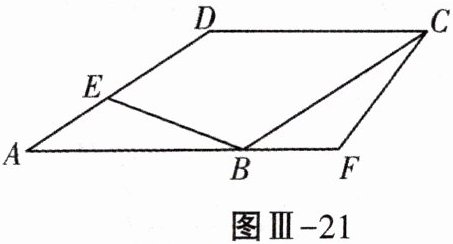
23. (8分)如图Ⅲ-21,在菱形ABCD中,点E是边AD上一点,延长AB至点F,使$BF= AE$,连接BE,CF.
求证:$BE= CF$.
证明:∵四边形$ ABCD $是菱形,
$ \therefore AB = BC $,$ AD // BC $,$ \therefore \angle A = \angle CBF $。
又$ \because AE = BF $,$ \therefore \triangle ABE \cong \triangle BCF $
求证:$BE= CF$.

证明:∵四边形$ ABCD $是菱形,
$ \therefore AB = BC $,$ AD // BC $,$ \therefore \angle A = \angle CBF $。
又$ \because AE = BF $,$ \therefore \triangle ABE \cong \triangle BCF $
(SAS)
,$ \therefore BE = CF $。
答案:
证明:
∵四边形$ ABCD $是菱形,
$ \therefore AB = BC $,$ AD // BC $,$ \therefore \angle A = \angle CBF $。
又$ \because AE = BF $,$ \therefore \triangle ABE \cong \triangle BCF $,$ \therefore BE = CF $。
∵四边形$ ABCD $是菱形,
$ \therefore AB = BC $,$ AD // BC $,$ \therefore \angle A = \angle CBF $。
又$ \because AE = BF $,$ \therefore \triangle ABE \cong \triangle BCF $,$ \therefore BE = CF $。
查看更多完整答案,请扫码查看


