2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若三角形三边长为 $ a、b、c $,$ (a+b)^{2}-c^{2}=2ab $,则此三角形是 (
A. 锐角三角形
B. 钝角三角形
C. 等腰直角三角形
D. 直角三角形
D
)A. 锐角三角形
B. 钝角三角形
C. 等腰直角三角形
D. 直角三角形
答案:
D
2. 如图,在 $ \text{Rt} \triangle ABC $ 中,$ \angle B=90^{\circ} $,以 $ AC $ 为直径的圆恰好过点 $ B $,$ AB=8 $,$ BC=6 $,则阴影部分的面积为 (
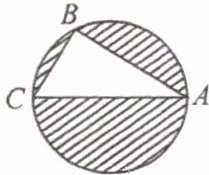
A. $ 100 \pi -24 $
B. $ 100 \pi -48 $
C. $ 25 \pi -24 $
D. $ 25 \pi -48 $
C
)
A. $ 100 \pi -24 $
B. $ 100 \pi -48 $
C. $ 25 \pi -24 $
D. $ 25 \pi -48 $
答案:
C
3. 两只小鼹鼠在地下打洞,一只朝前挖,每分钟挖 $ 8 \text{cm} $,一只朝左挖,每分钟挖 $ 6 \text{cm} $,10 分钟之后两只小鼹鼠相距为 (
A. $ 50 \text{cm} $
B. $ 100 \text{cm} $
C. $ 140 \text{cm} $
D. $ 80 \text{cm} $
B
)A. $ 50 \text{cm} $
B. $ 100 \text{cm} $
C. $ 140 \text{cm} $
D. $ 80 \text{cm} $
答案:
B
4. 如图,一只蚂蚁沿棱长为 $ a $ 的正方体表面从顶点 $ A $ 爬到顶点 $ B $,则它走过的最短路程为 (

A. $ \sqrt{3}a $
B. $ (1+\sqrt{2})a $
C. $ 3a $
D. $ \sqrt{5}a $
D
)
A. $ \sqrt{3}a $
B. $ (1+\sqrt{2})a $
C. $ 3a $
D. $ \sqrt{5}a $
答案:
D
5. 如图,在一个 $ 4 × 4 $ 个小正方形组成的正方形网格中,阴影部分与正方形 $ ABCD $ 面积之比是(
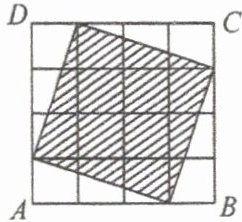
A. $ 3:4 $
B. $ 5:8 $
C. $ 9:16 $
D. $ 1:2 $
B
)
A. $ 3:4 $
B. $ 5:8 $
C. $ 9:16 $
D. $ 1:2 $
答案:
B
6. 分别以下列四组数为一个三角形的边长:① $ 6,8,10 $;② $ \frac{1}{3},\frac{1}{4},\frac{1}{5} $;③ $ 8,15,17 $;④ $ 4,5,6 $ 其中一定能构成直角三角形的有 (
A. 4 组
B. 3 组
C. 2 组
D. 1 组
C
)A. 4 组
B. 3 组
C. 2 组
D. 1 组
答案:
C
7. 在 $ \triangle ABC $ 中,$ AB=15 $,$ AC=13 $,高 $ AD=12 $,则 $ \triangle ABC $ 的周长是 (
A. 42
B. 32
C. 42 或 32
D. 37 或 33
C
)A. 42
B. 32
C. 42 或 32
D. 37 或 33
答案:
C
8. 如图,$ \triangle ABC $ 中,$ AD \perp BC $ 于 $ D $,$ AB=3 $,$ BD=2 $,$ DC=1 $,则 $ AC $ 的长为 (
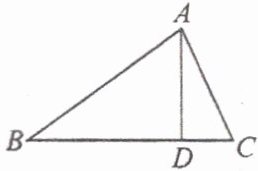
A. 6
B. $ \sqrt{6} $
C. $ \sqrt{5} $
D. 4
B
)
A. 6
B. $ \sqrt{6} $
C. $ \sqrt{5} $
D. 4
答案:
B
9. 如图,$ \triangle ABC $ 中,$ \angle C=90^{\circ} $,$ AD $ 平分 $ \angle BAC $,$ DE \perp AB $ 于 $ E $,下面等式错误的是 (
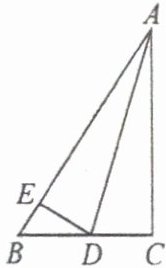
A. $ AC^{2}+DC^{2}=AD^{2} $
B. $ AD^{2}-DE^{2}=AE^{2} $
C. $ AD^{2}=DE^{2}+AC^{2} $
D. $ BD^{2}-BE^{2}=\frac{1}{4}BC^{2} $
D
)
A. $ AC^{2}+DC^{2}=AD^{2} $
B. $ AD^{2}-DE^{2}=AE^{2} $
C. $ AD^{2}=DE^{2}+AC^{2} $
D. $ BD^{2}-BE^{2}=\frac{1}{4}BC^{2} $
答案:
D
10. 如图,小明拿一张矩形纸图 1,沿虚线对折一次得到图 2,再将对角两顶点重合折叠得图 3,按图 4 沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是 (
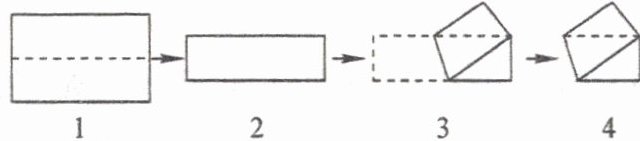
A. 都是等腰三角形
B. 都是等边三角形
C. 两个直角三角形,一个等腰三角形
D. 两个直角三角形,一个等腰梯形
C
)
A. 都是等腰三角形
B. 都是等边三角形
C. 两个直角三角形,一个等腰三角形
D. 两个直角三角形,一个等腰梯形
答案:
C
11. 如果直角三角形的斜边与一条直角边的长分别是 $ 13 \text{cm} $ 和 $ 5 \text{cm} $,那么这个直角三角形的面积是 ________
30
$ \text{cm}^{2} $。
答案:
30
12. 在 $ \triangle ABC $ 中,若 $ AC^{2}+AB^{2}=BC^{2} $,则 $ \angle B+\angle C= $
$90^{\circ}$
。
答案:
$90^{\circ}$
13. 若直角三角形的两边长分别为 $ 3 \text{cm},4 \text{cm} $,则第三边长为
$5\,\text{cm}$ 或 $\sqrt{7}\,\text{cm}$
。
答案:
$5cm$ 或 $\sqrt{7}cm$
查看更多完整答案,请扫码查看


