《2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社》

23. 如图,△ABC中,AB＞AC,AF是角平分线,D是AB上一点,且AD=AC,DE//BC交AC于E,求证:CD平分∠EDF.
证明：由题易得△ADF≌△ACF，∴DF=CF，∴∠FDC=∠FCD。∵DE//BC，∴∠EDC=∠FCD，∴∠FDC=∠EDC。即CD平分∠EDF。

答案： 由题易得 $\triangle ADF \cong \triangle ACF$，$\therefore DF = CF$，$\therefore \angle FDC = \angle FCD$。$\because DE // BC$，$\therefore \angle EDC = \angle FCD$，$\therefore \angle FDC = \angle EDC$。即 CD 平分 $\angle EDF$。

24. 如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.
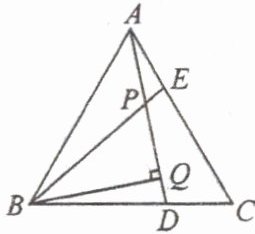
(1)求∠PBQ的度数.30°(2)判断PQ与BP的数量关系.PQ=1/2BP

答案： 解：$\because \triangle ABC$ 是等边三角形，
$\therefore AB = AC$，$\angle BAC = \angle C = 60^{\circ}$。
又 $\because AE = CD$，$\therefore \triangle ABE \cong \triangle ACD$，
$\therefore \angle ABE = \angle DAC$。
又 $\because \angle BPQ = \angle ABE + \angle BAD$，
$\therefore \angle BPQ = \angle DAC + \angle BAD = 60^{\circ}$，
$\therefore$ 在 $Rt\triangle BPQ$ 中，$\angle PBQ = 30^{\circ}$，
$\therefore PQ = \frac{1}{2}BP$。

25. 如图,为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:(1)分割后的整个图形必须是轴对称图形;(2)四块图形形状相同;(3)四块图形面积相等.现已有两种不同的分法:(1)分别作两条对角线(如图甲);(2)过一条边的四等分点作这边的垂线段(图乙)(图乙中两个图形的分割看作同一方法).请你按照上述三个要求,分别在下面两个正方形中给出另外两种不同的分割方法.(正确画图,不写画法)

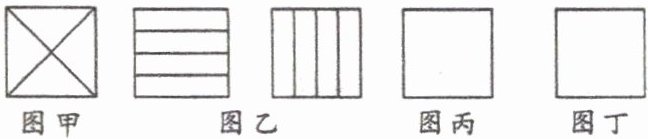
如图丙、丁

答案：
如图丙、丁