《2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社》

针对训练 2 如果梯子的底端离建筑物 9 米，那么 15 米长的梯子可以到达建筑物的高度是12米？

答案： 解:根据勾股定理 $AC^{2}+BC^{2}=AB^{2}$，即 $AC^{2}+9^{2}=15^{2}$，所以 $AC^{2}=144$，所以 $AC=12$。

【例 3】若 $ \triangle ABC $ 的三边长 $ a,b,c $ 满足 $ a^{2}+b^{2}+c^{2}+200=12a+16b+20c $，试判断 $ \triangle ABC $ 的形状。

答案： 【解析】：首先对已知等式进行变形，通过配方法将等式左边转化为完全平方式的和。因为完全平方式具有非负性，即任何数的平方都大于等于 0，而几个非负数的和为 0 时，那么这几个非负数都为 0，由此可求出三角形三边的长度。最后根据勾股定理的逆定理，若一个三角形的两条较短边的平方和等于最长边的平方，那么这个三角形就是直角三角形，从而判断出三角形的形状。
【答案】：直角三角形，且$\angle C = 90^{\circ}$

针对训练 3 如右图所示，在正方形 $ ABCD $ 中，$ F $ 为 $ DC $ 中点，$ E $ 为 $ BC $ 上一点，且 $ EC=\frac{1}{4}BC $。求证：$ \angle EFA=90^{\circ} $。

证明:设正方形边长为$4a$。
则 $EC=$$a$，$BE=$$3a$，$CF=FD=$$2a$。
在 $Rt\triangle ABE$ 中，由勾股定理得 $AE^{2}=AB^{2}+BE^{2}=$$16a^{2}$+$9a^{2}$=$25a^{2}$。
在 $Rt\triangle ADF$ 中，由勾股定理得
$AF^{2}=AD^{2}+DF^{2}=$$(4a)^{2}$+$(2a)^{2}$=$20a^{2}$。
在 $Rt\triangle CEF$ 中，$EF^{2}=CE^{2}+CF^{2}=$$a^{2}$+$4a^{2}$=$5a^{2}$。
在 $\triangle AEF$ 中，$AF^{2}+EF^{2}=$$20a^{2}$+$5a^{2}$=$25a^{2}$。
又因为 $AE^{2}=$$25a^{2}$，所以 $AF^{2}+EF^{2}=AE^{2}$，
所以 $\triangle AFE$ 为直角三角形，因为 $AE$ 为最大边，所以 $∠AFE = 90^{\circ}$。

答案： 证明:设正方形边长为 $4a$。
则 $EC=a$，$BE=3a$，$CF=FD=2a$。
在 $Rt\triangle ABE$ 中，由勾股定理得 $AE^{2}=AB^{2}+BE^{2}=16a^{2}+9a^{2}=25a^{2}$。
在 $Rt\triangle ADF$ 中，由勾股定理得
$AF^{2}=AD^{2}+DF^{2}=(4a)^{2}+(2a)^{2}=20a^{2}$。
在 $Rt\triangle CEF$ 中，$EF^{2}=CE^{2}+CF^{2}=a^{2}+4a^{2}=5a^{2}$。
在 $\triangle AEF$ 中，$AF^{2}+EF^{2}=20a^{2}+5a^{2}=25a^{2}$。
又因为 $AE^{2}=25a^{2}$，所以 $AF^{2}+EF^{2}=AE^{2}$，
所以 $\triangle AFE$ 为直角三角形，因为 $AE$ 为最大边，所以 $∠AFE = 90^{\circ}$。

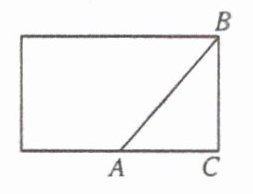
【例 4】如图，圆柱体的高为 20，底面半径 6.7，如果一只蚂蚁要自圆柱下面 $ A $ 点，沿侧面爬到与 $ A $ 相对的面上的 $ B $ 点，求爬行的最短路线的长度。

29

答案：
【解析】：将圆柱体侧面展开，在$Rt\triangle ABC$中，$BC$为圆柱的高$20$，$AC$为底面周长的一半，根据圆的周长公式$C = 2\pi r$（$r$为半径）算出$AC\approx21$，再利用勾股定理$AB^{2}=AC^{2}+BC^{2}$求出$AB$的长度。

【答案】：$29$

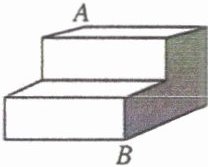
针对训练 4 如图，它是一个二级台阶，每一级的长、宽、高分别为 $ 60 \text{cm},30 \text{cm},10 \text{cm} $，$ A $ 和 $ B $ 是这个台阶的两个相对的端点，$ A $ 点上有一只蚂蚁，想到 $ B $ 点去吃可口的食物，请你帮助小蚂蚁计算一下，沿着台阶从 $ A $ 到 $ B $ 最短爬行路程是100cm。

答案：
把台阶面如图所示摊平、展开，四个面合成一个长方形，$A$，$B$ 两点间的最短路线就是 $AB$，又在 $Rt\triangle ABC$ 中，$AC = 30×2 + 10×2 = 80(cm)$，$BC = 60(cm)$，由勾股定理，得 $AB^{2}=AC^{2}+BC^{2}=80^{2}+60^{2}=10000$。解得 $AB = 100(cm)$。