《2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社》

14. 如果 $ \triangle ABC $ 的三边长 $ a、b、c $ 满足关系式 $ (a+2b-60)^{2}+|b-18|+\sqrt{c-30}=0 $，则 $ \triangle ABC $ 是 直角 三角形。

答案： 直角

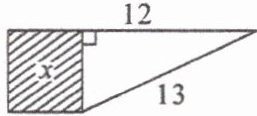
15. 下图中阴影部分的面积 $ x= $ 25。

答案： 25

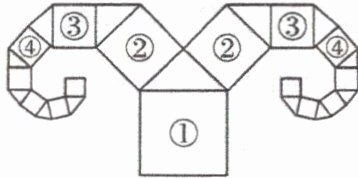
16. 如图，是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以直角边为边，分别向外作正方形……，依此类推，若正方形①的边长为 64，则正方形⑦的边长为 8。

答案： 8

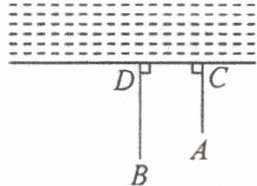
17. 如图，一牧童在 $ A $ 处牧马，牧童家在 $ B $ 处，$ A、B $ 处距河岸的距离 $ AC,BD $ 的长分别为 500 米和 700 米，且 $ CD=500 $ 米，天黑前牧童从 $ A $ 点将马牵到河边去饮水后，再赶回家，那么牧童最少要走 1300 米。

答案： 1300

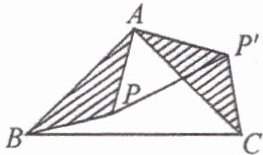
18. 如图，$ ABC $ 是直角三角形，$ BC $ 是斜边，将 $ \triangle ABP $ 绕点 $ A $ 逆时针旋转后，能与 $ \triangle ACP' $ 重合，如果 $ AP=3 $，那么 $ PP'= $ $3\sqrt{2}$。

答案： $3\sqrt{2}$

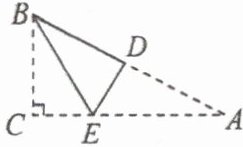
19. 如图，在三角形纸片 $ ABC $ 中，$ \angle C=90^{\circ} $，$ \angle A=30^{\circ} $，$ AC=3 $，折叠该纸片，使点 $ A $ 与点 $ B $ 重合，折痕与 $ AB、AC $ 分别相交于点 $ D $ 和点 $ E $，折痕 $ DE $ 的长为 1。

答案： 1

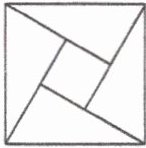
20. 如图，是在北京召开的国际数学大会的会标，它是由四个相同的直角三角形与中间一个小正方形拼成的一个大正方形。若大正方形的边长是 $ 13 \text{cm} $，小正方形的边长为 $ 7 \text{cm} $，则每个直角三角形较短的一条直角边的长是 5 $ \text{cm} $。

答案： 5

三、解答题。
21. 已知：$ a,b,c $ 为 $ \triangle ABC $ 的三边，且满足 $ a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4} $，试判断 $ \triangle ABC $ 的形状。

答案： 21. 解: $ \because a^{2}c^{2}-b^{2}c^{2}=a^{4}-b^{4} $，
$ \therefore (a^{2}-b^{2})c^{2}=(a^{2}+b^{2})(a^{2}-b^{2}) $，
$ \therefore (a^{2}-b^{2})(a^{2}+b^{2}-c^{2})=0 $，
$ \therefore a^{2}-b^{2}=0 $ 或 $ a^{2}+b^{2}-c^{2}=0 $，
即 $ a=b $ 或 $ a^{2}+b^{2}=c^{2} $。
$ \therefore \triangle ABC $ 的形状为等腰三角形或直角三角形。

22. 如图，为修通铁路需凿通隧道 $ AC $，量出 $ \angle A=40^{\circ} $，$ \angle B=50^{\circ} $，$ AB=5 $ 千米，$ BC=4 $ 千米，若每天凿隧道 0.3 千米，问几天才能把隧道 $ AB $ 凿通？

10 天

答案： 22. 10 天

23. 如图，$ \triangle ABC $ 中，$ AB=13 $，$ BC=10 $，中线 $ AD=12 $，求证：$ AB=AC $。
证明: $ \because AD $ 为中线，$ \therefore BD=DC= $5，
在 $ \triangle ABD $ 中，$ \because $$ 12^{2}+5^{2}=13^{2} $，
即$ AB^{2}=AD^{2}+BD^{2} $，
$ \therefore \angle ADB= $$ 90^{\circ} $，
$ \therefore AD $ 垂直平分 $ BC $，
$ \therefore AB=AC $。

答案： 23. 证明: $ \because AD $ 为中线，$ \therefore BD=DC=5 $，
在 $ \triangle ABD $ 中，$ \because 12^{2}+5^{2}=13^{2} $，
即 $ AB^{2}=AD^{2}+BD^{2} $，
$ \therefore \angle ADB=90^{\circ} $，
$ \therefore AD $ 垂直平分 $ BC $，
$ \therefore AB=AC $。

24. 如图，在四边形 $ ABCD $ 中，$ AB=AD=8 $，$ \angle A=60^{\circ} $，$ \angle ADC=150^{\circ} $，已知四边形 $ ABCD $ 的周长为 32，求四边形 $ ABCD $ 的面积。

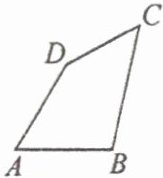
$16\sqrt{3}+24$

答案： 24. 连接 $ BD $。因为 $ AB=AD $，$ \angle A=60^{\circ} $，所以 $ \triangle ABD $ 是等边三角形。所以 $ \angle ADB=60^{\circ} $，$ BD=AB=AD=8 $。因为 $ \angle ADC=150^{\circ} $，所以 $ \angle BDC=90^{\circ} $，即 $ \triangle BDC $ 是直角三角形。因为四边形 $ ABCD $ 的周长为 32，$ AB=AD=8 $，所以 $ BC+DC=32 - 16 = 16 $，$ BC = 16 - DC $。在 $ Rt\triangle BDC $ 中，$ BD^{2}+DC^{2}=BC^{2} $ 即 $ 8^{2}+DC^{2}=(16 - DC)^{2} $。解得 $ DC = 6 $。所以 $ S_{\triangle BDC}=\frac{1}{2}×6×8 = 24 $。用勾股定理求出等边三角形 $ ABD $ 的高为 $ \sqrt{8^{2}-(\frac{8}{2})^{2}}=4\sqrt{3} $。所以 $ S_{\triangle ABD}=\frac{1}{2}×8×4\sqrt{3}=16\sqrt{3} $。所以 $ S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BDC}=16\sqrt{3}+24 $。

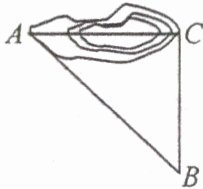
25. 台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形成气旋风暴，有极强的破坏力，据气象观测，距沿海某城市 $ A $ 的正南方向 240 千米的 $ B $ 处有一台风中心，其中心风力为 12 级，每远离台风中心 25 千米，风力就会减弱一级，该台风中心现正以 20 千米/时的速度沿此偏东 $ 30^{\circ} $ 的方向往 $ C $ 移动，如图，且台风中心的风力不变，若城市所受风力达到或超过 4 级，则称受台风影响。
(1) 该城市是否受台风的影响？请说明理由。
(2) 若会受到台风影响，那么台风影响城市的持续时间有多长？16小时
(3) 该城市受到台风影响的最大风力为几级？7.2级

答案：
25. 解:
(1)该城市受到台风的影响. 理由:过点 $ A $ 作 $ AD \perp BC $ 于 $ D $ 点，在 $ Rt\triangle ABD $ 中，$ \angle ABD=30^{\circ} $，则 $ AD=\frac{1}{2}AB=\frac{1}{2}×240 = 120 $ (千米)，又受到台风影响的最大距离 $ 25×(12 - 4)=200 $ (千米)，$ 120＜200 $，所以该城市受到台风影响。
(2)设台风中心由 $ B $ 移至点 $ E $ 时，该城市开始受到台风影响，台风中心再移至点 $ C $ 时，该城市脱离台风影响，则 $ AE=AC=200 $ (千米)。在 $ Rt\triangle ADE $ 中，由勾股定理得 $ DE^{2}=AE^{2}-AD^{2}=200^{2}-120^{2}=160^{2} $，$ \therefore DE = 160 $ (千米)，同理可求出 $ DC = 160 $ (千米)。所以该城市受台风影响的时间为 $ \frac{160×2}{20}=16 $ (小时)
(3)当台风中心位于 $ D $ 处时，对城市 $ A $ 的影响最大，
因为 $ AD = 120 $ 千米，所以台风从 $ D $ 到 $ A $，其风力将减弱 $ \frac{120}{25}=4.8 $ (级)
所以 $ 12 - 4.8 = 7.2 $ (级)。所以该城市受到台风影响的最大风力为 $ 7.2 $ 级。