《2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社》

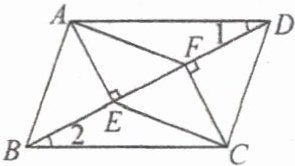
【例1】如图，在$□ ABCD$中，$AE\perp BD$，垂足为$E$，$CF\perp BD$，垂足为$F$，求证：四边形$AECF$为平行四边形。

答案： 【剖析】要证四边形$AECF$是平行四边形。
需要找条件，由已知可以知道：找一组对边平行且相等较简单。
【解答】证明：$\because$四边形$ABCD$是平行四边形，
$\therefore AD = BC$，$AD// BC$，
$\therefore\angle 1=\angle 2$。
$\because AE\perp BD$于$E$，$CF\perp BD$于$F$，
$\therefore\angle AED=\angle CFB = 90^{\circ}$，$AE// CF$，
$\therefore\triangle AED\cong\triangle CFB$，$\therefore AE = CF$。
又$AE// CF$，$\therefore$四边形$AECF$是平行四边形。

针对训练1 如图，在$□ ABCD$中，$BN = MD$，$BE = DF$，求证：四边形$MENF$是平行四边形。
证明：∵四边形$ABCD$是平行四边形，
∴$AD // BC$，
∴$∠EBN = ∠FDM$。
又$BN = MD$，$BE = DF$，∴$△EBN \cong △FDM$，∴$EN = FM$，
$∠BEN = ∠DFM$。
∴$∠MFE = ∠FEN$。
∴$EN // MF$，又$EN = FM$，
∴四边形$MENF$是平行四边形。

答案： 证明：
∵四边形 $ABCD$ 是平行四边形，
∴ $AD // BC$，
∴ $∠EBN = ∠FDM$。
又 $BN = MD$，$BE = DF$，
∴ $△EBN \cong △FDM$，
∴ $EN = FM$，
$∠BEN = ∠DFM$。
∴ $∠MFE = ∠FEN$。
∴ $EN // MF$，又 $EN = FM$，
∴四边形 $MENF$ 是平行四边形。