2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. (杭州)如图,在$□ ABCD$中,下列结论一定正确的是(

A. $AC\perp BD$
B. $\angle A+\angle B = 180^{\circ}$
C. $AB = AD$
D. $\angle A\neq\angle C$
B
)
A. $AC\perp BD$
B. $\angle A+\angle B = 180^{\circ}$
C. $AB = AD$
D. $\angle A\neq\angle C$
答案:
B
2. (江西)如图,$□ ABCD$与$□ DCFE$的周长相等,且$\angle BAD = 60^{\circ}$,$\angle F = 110^{\circ}$,则$\angle DAE$的度数为______

25°
。
答案:
$25^\circ$
3. (河南)如图,在矩形$ABCD$中,$AB = 3$,$BC = 4$,点$E$是$BC$边上一点,连接$AE$,把$\angle B$沿$AE$折叠,使点$B$落在点$B'$处。当$\triangle CEB'$为直角三角形时,$BE$的长为

$\frac{3}{2}$ 或 3
。
答案:
$\frac{3}{2}$ 或 3
4. (江西)如图,在矩形$ABCD$中,点$E$,$F$分别是$AB$,$CD$的中点,连接$DE$和$BF$,分别取$DE$,$BF$的中点$M$,$N$,连接$AM$,$CN$,$MN$,若$AB = 2\sqrt{2}$,$BC = 2\sqrt{3}$,则图中阴影部分的面积为

$2\sqrt{6}$
。
答案:
$2\sqrt{6}$
5. (莱芜)如图,在矩形$ABCD$中,$AB = 1$,$E$、$F$分别为$AD$、$CD$的中点,沿$BE$将$\triangle ABE$折叠,若点$A$恰好落在$BF$上,则$AD=$
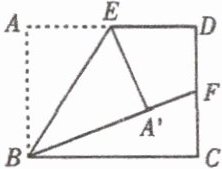
$\sqrt{2}$
。
答案:
$\sqrt{2}$
6. (莱芜)如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,以$AC$为一边向外作等边三角形$ACD$,点$E$为$AB$的中点,连接$DE$。
(1) 证明:$DE// CB$;
(2) 探索$AC$与$AB$满足怎样的数量关系时,四边形$DCBE$是平行四边形。
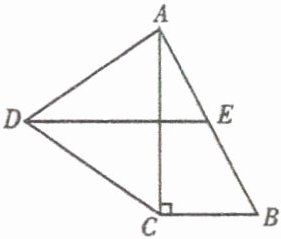
(1)证明:如图,连接 $CE$,∵ $E$ 为 $Rt△ACB$ 的斜边 $AB$ 的中点,
∴ $CE = \frac{1}{2}AB = AE$。
∵ $△ACD$ 是等边三角形,∴ $AD = CD$。
在 $△ADE$ 和 $△CDE$ 中,
$AD = CD$,$DE = DE$,$AE = CE$,
∴ $△ADE \cong △CDE(SSS)$。
∴ $∠ADE = ∠CDE = 30^\circ$。
∵ $∠DCB = ∠ACB + ∠ACD = 90^\circ + 60^\circ = 150^\circ$,
∴ $∠EDC + ∠DCB = 180^\circ$,
∴ $DE // CB$。
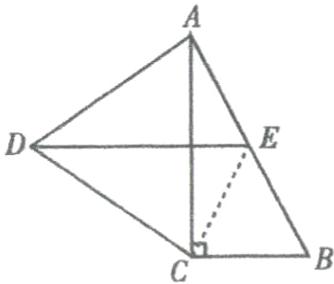
(2)解:∵ $∠DCB = 150^\circ$,
若四边形 $DCBE$ 是平行四边形,则 $DC // BE$,$∠DCB + ∠B = 180^\circ$,
∴ $∠B = 30^\circ$。
在 $Rt△ACB$ 中,$∠B = 30^\circ$,∴ $AC = \frac{1}{2}AB$ 或 $AB = 2AC$,
∴当 $AC =$
(1) 证明:$DE// CB$;
(2) 探索$AC$与$AB$满足怎样的数量关系时,四边形$DCBE$是平行四边形。

(1)证明:如图,连接 $CE$,∵ $E$ 为 $Rt△ACB$ 的斜边 $AB$ 的中点,
∴ $CE = \frac{1}{2}AB = AE$。
∵ $△ACD$ 是等边三角形,∴ $AD = CD$。
在 $△ADE$ 和 $△CDE$ 中,
$AD = CD$,$DE = DE$,$AE = CE$,
∴ $△ADE \cong △CDE(SSS)$。
∴ $∠ADE = ∠CDE = 30^\circ$。
∵ $∠DCB = ∠ACB + ∠ACD = 90^\circ + 60^\circ = 150^\circ$,
∴ $∠EDC + ∠DCB = 180^\circ$,
∴ $DE // CB$。

(2)解:∵ $∠DCB = 150^\circ$,
若四边形 $DCBE$ 是平行四边形,则 $DC // BE$,$∠DCB + ∠B = 180^\circ$,
∴ $∠B = 30^\circ$。
在 $Rt△ACB$ 中,$∠B = 30^\circ$,∴ $AC = \frac{1}{2}AB$ 或 $AB = 2AC$,
∴当 $AC =$
$\frac{1}{2}AB$
或 $AB =$$2AC$
时,四边形 $DCBE$ 是平行四边形。
答案:
(1)证明:如图,连接 $CE$,
∵ $E$ 为 $Rt△ACB$ 的斜边 $AB$ 的中点,
∴ $CE = \frac{1}{2}AB = AE$。
∵ $△ACD$ 是等边三角形,
∴ $AD = CD$。
在 $△ADE$ 和 $△CDE$ 中,
$AD = CD$,$DE = DE$,$AE = CE$,
∴ $△ADE \cong △CDE(SSS)$。
∴ $∠ADE = ∠CDE = 30^\circ$。
∵ $∠DCB = ∠ACB + ∠ACD = 90^\circ + 60^\circ = 150^\circ$,
∴ $∠EDC + ∠DCB = 180^\circ$,
∴ $DE // CB$。

(2)解:
∵ $∠DCB = 150^\circ$,
若四边形 $DCBE$ 是平行四边形,则 $DC // BE$,$∠DCB + ∠B = 180^\circ$,
∴ $∠B = 30^\circ$。
在 $Rt△ACB$ 中,$∠B = 30^\circ$,
∴ $AC = \frac{1}{2}AB$ 或 $AB = 2AC$,
∴当 $AC = \frac{1}{2}AB$ 或 $AB = 2AC$ 时,四边形 $DCBE$ 是平行四边形。
(1)证明:如图,连接 $CE$,
∵ $E$ 为 $Rt△ACB$ 的斜边 $AB$ 的中点,
∴ $CE = \frac{1}{2}AB = AE$。
∵ $△ACD$ 是等边三角形,
∴ $AD = CD$。
在 $△ADE$ 和 $△CDE$ 中,
$AD = CD$,$DE = DE$,$AE = CE$,
∴ $△ADE \cong △CDE(SSS)$。
∴ $∠ADE = ∠CDE = 30^\circ$。
∵ $∠DCB = ∠ACB + ∠ACD = 90^\circ + 60^\circ = 150^\circ$,
∴ $∠EDC + ∠DCB = 180^\circ$,
∴ $DE // CB$。

(2)解:
∵ $∠DCB = 150^\circ$,
若四边形 $DCBE$ 是平行四边形,则 $DC // BE$,$∠DCB + ∠B = 180^\circ$,
∴ $∠B = 30^\circ$。
在 $Rt△ACB$ 中,$∠B = 30^\circ$,
∴ $AC = \frac{1}{2}AB$ 或 $AB = 2AC$,
∴当 $AC = \frac{1}{2}AB$ 或 $AB = 2AC$ 时,四边形 $DCBE$ 是平行四边形。
7. (黄冈)如图,四边形$ABCD$是菱形,对角线$AC$,$BD$相交于点$O$,$DH\perp AB$于点$H$,连接$OH$,求证:$\angle DHO=\angle DCO$。
证明:∵四边形 $ABCD$ 是菱形,
∴
∵ $DH \perp AB$ 于点 $H$,
∴
∴
∴
∴
在 $Rt△COD$ 中,
在 $Rt△DHB$ 中,
∴ $∠DHO = ∠DCO$。
证明:∵四边形 $ABCD$ 是菱形,
∴
$OD = OB$
,$∠COD = 90^\circ$
,$∠ODC = ∠OBH$
。∵ $DH \perp AB$ 于点 $H$,
∴
$∠DHB = 90^\circ$
。∴
$HO = \frac{1}{2}BD = OB$
,∴
$∠OHB = ∠OBH$
。∴
$∠OHB = ∠ODC$
。在 $Rt△COD$ 中,
$∠ODC + ∠DCO = 90^\circ$
。在 $Rt△DHB$ 中,
$∠DHO + ∠OHB = 90^\circ$
。∴ $∠DHO = ∠DCO$。
答案:
证明:
∵四边形 $ABCD$ 是菱形,
∴ $OD = OB$,$∠COD = 90^\circ$,$∠ODC = ∠OBH$。
∵ $DH \perp AB$ 于点 $H$,
∴ $∠DHB = 90^\circ$。
∴ $HO = \frac{1}{2}BD = OB$,
∴ $∠OHB = ∠OBH$。
∴ $∠OHB = ∠ODC$。
在 $Rt△COD$ 中,$∠ODC + ∠DCO = 90^\circ$。
在 $Rt△DHB$ 中,$∠DHO + ∠OHB = 90^\circ$。
∴ $∠DHO = ∠DCO$。
∵四边形 $ABCD$ 是菱形,
∴ $OD = OB$,$∠COD = 90^\circ$,$∠ODC = ∠OBH$。
∵ $DH \perp AB$ 于点 $H$,
∴ $∠DHB = 90^\circ$。
∴ $HO = \frac{1}{2}BD = OB$,
∴ $∠OHB = ∠OBH$。
∴ $∠OHB = ∠ODC$。
在 $Rt△COD$ 中,$∠ODC + ∠DCO = 90^\circ$。
在 $Rt△DHB$ 中,$∠DHO + ∠OHB = 90^\circ$。
∴ $∠DHO = ∠DCO$。
查看更多完整答案,请扫码查看


