2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. 矩形的面积为$120cm^{2}$,周长为$46cm$,则它的对角线长为(
A. $15cm$
B. $16cm$
C. $17cm$
D. $18cm$
C
)A. $15cm$
B. $16cm$
C. $17cm$
D. $18cm$
答案:
C
4. $A$、$B$、$C$、$D$在同一平面内,从①$AB// CD$;②$AB = CD$;③$BC// AD$;④$BC = AD$。这四个条件中任选两个,能使四边形$ABCD$成为平行四边形的选法共有(
A. $3$种
B. $4$种
C. $5$种
D. $6$种
B
)A. $3$种
B. $4$种
C. $5$种
D. $6$种
答案:
B
5. 如图,过矩形$ABCD$的四个顶点作对角线$AC$、$BD$的平行线,分别相交于$E$、$F$、$G$、$H$四点,则四边形$EFGH$为(
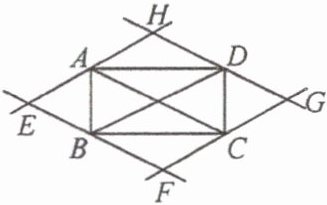
A. 平行四边形
B. 矩形
C. 菱形
D. 正方形
C
)
A. 平行四边形
B. 矩形
C. 菱形
D. 正方形
答案:
C
6. 在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是(
A. 测量对角线是否相互平分
B. 测量两组对边是否分别相等
C. 测量一组对角是否都为直角
D. 测量其中三个内角是否都为直角
D
)A. 测量对角线是否相互平分
B. 测量两组对边是否分别相等
C. 测量一组对角是否都为直角
D. 测量其中三个内角是否都为直角
答案:
D
7. 如图,在正方形$ABCD$中,$E$为$DC$边上的点,连接$BE$,将$\triangle BCE$绕点$C$顺时针方向旋转$90^{\circ}$得到$\triangle DCF$,连接$EF$。若$\angle BEC = 60^{\circ}$,则$\angle EFD$的度数为(
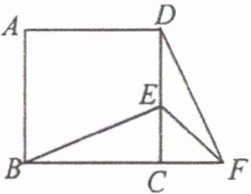
A. $10^{\circ}$
B. $15^{\circ}$
C. $20^{\circ}$
D. $25^{\circ}$
B
)
A. $10^{\circ}$
B. $15^{\circ}$
C. $20^{\circ}$
D. $25^{\circ}$
答案:
B
8. 矩形、菱形、正方形都具有的性质是(
A. 对角线相等
B. 对角线互相平分
C. 对角线互相垂直
D. 对角线平分对角
B
)A. 对角线相等
B. 对角线互相平分
C. 对角线互相垂直
D. 对角线平分对角
答案:
B
9. 如图,已知正方形$ABCD$的顶点$C$落在与其大小相同的正方形$PQRS$的对称中心位置上,当$ABCD$绕点$C$旋转时,设这两个图形重叠部分的面积为$S_{1}$,正方形$PQRS$的面积为$S_{2}$,则$S_{1}$与$S_{2}$的关系是(
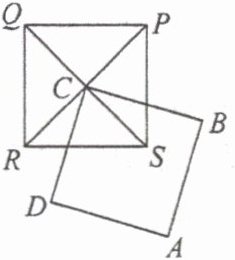
A. $S_{2}=2S_{1}$
B. $S_{2}=3S_{1}$
C. $S_{2}=4S_{1}$
D. $2S_{2}=5S_{1}$
C
)
A. $S_{2}=2S_{1}$
B. $S_{2}=3S_{1}$
C. $S_{2}=4S_{1}$
D. $2S_{2}=5S_{1}$
答案:
C
10. 如图,已知四边形$ABCD$,则在下列结论中,能推出四边形$ABCD$为正方形的有(
①四边形$ABCD$是平行四边形,且$AB\perp BC$;
②四边形$ABCD$是平行四边形,且$AC\perp BD$;
③四边形$ABCD$是矩形,且$AC\perp BD$;
④四边形$ABCD$是菱形,且$AC = BD$。
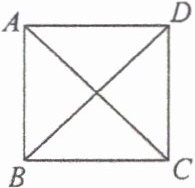
A. ①,②
B. ②,③
C. ③,④
D. ①,②,③,④
C
)①四边形$ABCD$是平行四边形,且$AB\perp BC$;
②四边形$ABCD$是平行四边形,且$AC\perp BD$;
③四边形$ABCD$是矩形,且$AC\perp BD$;
④四边形$ABCD$是菱形,且$AC = BD$。

A. ①,②
B. ②,③
C. ③,④
D. ①,②,③,④
答案:
C
11. 平行四边形的周长等于$56cm$,两邻边长的比为$3:1$,那么这个平行四边形较长的边长为
$21cm$
。
答案:
$21cm$
12. 平行四边形$ABCD$,加一个条件
四条边相等
,它就是菱形。
答案:
四条边相等
13. 若菱形的周长为$24cm$,一个内角为$60^{\circ}$,则菱形的面积为
$18\sqrt{3}$
$cm^{2}$。
答案:
$18\sqrt{3}$
14. 一个菱形的两条对角线长分别为$6cm$,$8cm$,这个菱形的边长为
$5cm$
,面积$S=$$24cm^2$
。
答案:
$5cm$ $24cm^2$
15. 在$□ ABCD$中,两邻边的差为$4cm$,周长为$32cm$,则两邻边长分别为
$10cm$,$6cm$
。
答案:
$10cm$ $6cm$
16. 已知菱形$ABCD$的边长为$6$,$\angle A = 60^{\circ}$,如果点$P$是菱形内一点,且$PB = PD = 2\sqrt{3}$,那么$AP$的长为
$2\sqrt{3}$ 或 $4\sqrt{3}$
。
答案:
$2\sqrt{3}$ 或 $4\sqrt{3}$
查看更多完整答案,请扫码查看


