2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 计算$(-a)^{3}\cdot (a^{2})^{3}\cdot (-a)^{2}$的结果正确的是(
A. $a^{11}$
B. $-a^{11}$
C. $-a^{10}$
D. $a^{13}$
B
)A. $a^{11}$
B. $-a^{11}$
C. $-a^{10}$
D. $a^{13}$
答案:
B
2. 下列计算正确的是(
A. $x^{2(m+1)}÷x^{m+1}=x^{2}$
B. $(xy)^{8}÷(xy)^{4}=(xy)^{2}$
C. $x^{10}÷(x^{7}÷x^{2})=x^{5}$
D. $x^{4n}÷x^{2n}\cdot x^{2n}=1$
C
)A. $x^{2(m+1)}÷x^{m+1}=x^{2}$
B. $(xy)^{8}÷(xy)^{4}=(xy)^{2}$
C. $x^{10}÷(x^{7}÷x^{2})=x^{5}$
D. $x^{4n}÷x^{2n}\cdot x^{2n}=1$
答案:
C
3. $4^{m}\cdot 4^{n}$的结果是(
A. $2^{2(m+n)}$
B. $16^{mn}$
C. $4^{mn}$
D. $16^{m+n}$
A
)A. $2^{2(m+n)}$
B. $16^{mn}$
C. $4^{mn}$
D. $16^{m+n}$
答案:
A
4. 若$a$为正整数,且$x^{2a}=5$,则$(2x^{3a})^{2}÷4x^{4a}$的值为(
A. 5
B. $\frac {5}{2}$
C. 25
D. 10
A
)A. 5
B. $\frac {5}{2}$
C. 25
D. 10
答案:
A
5. 下列算式中,正确的是(
A. $(a^{2}b^{3})^{5}÷(ab^{2})^{10}=ab^{5}$
B. $(\frac {1}{3})^{-2}=\frac {1}{3^{2}}=\frac {1}{9}$
C. $(0.00001)^{0}=(9999)^{0}$
D. $3.24×10^{-4}=0.0000324$
C
)A. $(a^{2}b^{3})^{5}÷(ab^{2})^{10}=ab^{5}$
B. $(\frac {1}{3})^{-2}=\frac {1}{3^{2}}=\frac {1}{9}$
C. $(0.00001)^{0}=(9999)^{0}$
D. $3.24×10^{-4}=0.0000324$
答案:
C
6. $(-a+1)(a+1)(a^{2}+1)$等于(
A. $a^{4}-1$
B. $a^{4}+1$
C. $a^{4}+2a^{2}+1$
D. $1-a^{4}$
D
)A. $a^{4}-1$
B. $a^{4}+1$
C. $a^{4}+2a^{2}+1$
D. $1-a^{4}$
答案:
D
7. 若$(x+m)(x-8)$中不含$x$的一次项,则$m$的值为(
A. 8
B. -8
C. 0
D. 8或-8
A
)A. 8
B. -8
C. 0
D. 8或-8
答案:
A
8. 已知$a+b=10$,$ab=24$,则$a^{2}+b^{2}$的值是(
A. 148
B. 76
C. 58
D. 52
D
)A. 148
B. 76
C. 58
D. 52
答案:
D
9. 已知多项式$ax^{2}+bx+c$因式分解的结果为$(x-1)(x+4)$,则$abc$的值为(
A. 12
B. 9
C. -9
D. -12
D
)A. 12
B. 9
C. -9
D. -12
答案:
D
10. 如图,矩形花园$ABCD$中,$AB=a$,$AD=b$,花园中建有一条矩形道路$LMPQ$及一条平行四边形道路$RSTK$.若$LM=RS=c$,则花园中可绿化部分的面积为(
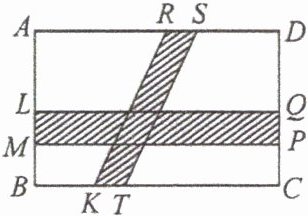
A. $bc-ab+ac+b^{2}$
B. $a^{2}+ab+bc-ac$
C. $ab-bc-ac+c^{2}$
D. $b^{2}-bc+a^{2}-ab$
C
)
A. $bc-ab+ac+b^{2}$
B. $a^{2}+ab+bc-ac$
C. $ab-bc-ac+c^{2}$
D. $b^{2}-bc+a^{2}-ab$
答案:
C
11. ①$a^{2}-4a+4$,②$a^{2}+a+\frac {1}{4}$,③$4a^{2}-a+\frac {1}{4}$,④$4a^{2}+4a+1$,以上各式中属于完全平方式的有
①②④
(填序号).
答案:
①②④
12. $(4a^{2}-b^{2})÷(b-2a)=$
$-2a - b$
.
答案:
$-2a - b$
13. 若$x+y=8$,$x^{2}y^{2}=4$,$(x>0,y>0)$则$x^{2}+y^{2}=$
60
.
答案:
60
14. 计算:$83^{2}+83×34+17^{2}=$
10000
.
答案:
10000
15. $(12a^{2m+1}b^{m+3}-20a^{m+1}b^{2m+4}+4a^{m+1}b^{m+2})÷4a^{m}b^{m+1}=$
$3a^{m + 1}b^2 - 5ab^{m + 3} + ab$
.
答案:
$3a^{m + 1}b^2 - 5ab^{m + 3} + ab$
16. 已知$x^{2}-y^{2}=12$,$x-y=2$,则$\frac {x}{y}=$
2
.
答案:
2
17. 代数式$4x^{2}+3mx+9$是完全平方式,则$m=$
$\pm 4$
.
答案:
$\pm 4$
18. 若$|a-2|+b^{2}-2b+1=0$,则$a=$
2
,$b=$1
.
答案:
2 1
19. 已知正方形的面积是$9x^{2}+6xy+y^{2}(x>0,y>0)$,利用分解因式,写出表示该正方形的边长的代数式
$3x + y$
.
答案:
$3x + y$
查看更多完整答案,请扫码查看


